Gassendi lecteur de Galilée

Nous n'hésiterons pas à voir, dans cette assertion, le comble de l'ineptie. Aux fins d'accréditer cette idée, nous confronterons l'assertion aux principaux textes dans lesquels les contemporains ont réfléchi la découverte de la rotation du Soleil et de l'inclinaison de son plan de rotation au plan de l'écliptique. Nous trouverons qu'à l'inverse de Scheiner et de Galilée (l'ouvrage de Hevelius n'étant pas paru à la date de la rédaction), Gassendi rattache les stationes, aux équinoxes, et les aequilibria, aux solstices. Il croit, à tort, que la rotation du Soleil s'accomplit dans le plan de l'écliptique. Il attribue, de ce fait, les variations qui affectent les trajectoires apparentes des taches, non à l'obliquité du plan de rotation du Soleil, à l'égard de l'écliptique, mais à celle de l'écliptique, à l'égard de l'équateur céleste, donc, à la position de l'observateur par rapport au Soleil, ce qui est une lecture bien hâtive de la Terza Giornata. A contrario, Riccioli écrira, dans un ouvrage publié en 1651 : « Que le grand cercle du corps du Soleil, dans lequel, et dans les parallèles duquel, se fait cette rotation, est incliné à l'Ecliptique d'une façon telle que le mouvement apparent des Taches paraît tracer, dans les Equinoxes, des lignes droites, et en dehors des Equinoxes, des lignes courbes, telle est l'opinion de Gassendi, alors que Scheiner affirme, au contraire, que, près des Solstices, ces taches décrivent des droites, et dans les Equinoxes ou ailleurs, des courbes, ce qui provient, selon lui, d'un certain mouvement annuel distinct, qui ne se confond pas avec le mouvement mensuel et par lequel les pôles du mouvement mensuel, ainsi que son axe, sont sensiblement affectés. » (2). Toutefois, c'est à tort que Riccioli attribue à Gassendi l'idée d'un plan de rotation du Soleil distinct de celui de l'écliptique ; une première erreur logique et optique de Gassendi consiste, précisément, à ne pas se souvenir que, le centre du Soleil et le centre de la Terre étant, par définition, dans le plan de l'écliptique, toute section du globe solaire par un plan orthogonal à l'axe du cône visuel de l'observateur terrestre est, nécessairement, dans un plan orthogonal au plan de l'écliptique (en négligeant la parallaxe). En pensant que la rotation du Soleil s'accomplit dans ce plan, Gassendi s'en tient à une position de Galilée antérieure à la publication du Dialogo, telle qu'elle s'exprime dans l'Istoria e dimostrazioni intorno alle macchie solari de 1613 : « Rappresentandocisi i progressi di tutte le macchie sotto specie di linee rette (argomento necessario, l'asse di tale conversioni esser eretto al piano che passa per i centri del Sole) ... » (3). A cette date, Galilée conclut correctement que, si la rotation du Soleil s'accomplit dans le plan de l'écliptique, comme il le suppose encore à la date où il écrit ce texte, daté du 14 août 1612, les traversées apparentes des taches se font, nécessairement, toujours en ligne droite. La courbure de leurs trajectoires ne résulte que d'observations ultérieures. Et lorsque, dans ce texte de 1642, Gassendi écrit : « Et cela ne saurait, dit-il, mieux s'expliquer que par la raison que, le Soleil tournant toujours sur les mêmes Pôles qui lui sont propres, ou Pôles de l'Ecliptique, en entraînant les Taches, la Terre se place, par rapport à lui, tantôt, comme sur sa droite ou sur sa gauche, dans les équinoxes, tantôt, au-dessus ou en-dessous, dans les solstices, d'une façon telle que, selon qu'il lui présente telle ou telle conformation de son axe, elle voit s'avancer les Taches dans le disque du Soleil, non pas d'une seule et même façon, mais avec les différentes formes de droites et de courbes que nous évoquions. » (4), l'origine de cette erreur pourrait bien résider dans un faux-sens sur l'expression « circa summitatem borealem & depressionem » dans un texte de Scheiner publié en 1630 : « ce qui fait que le Soleil, aux alentours de son sommet Nord et de sa base Sud, incline la tête vers la terre l'espace de six mois, puis, la relève par rapport à elle, par l'effet de la présence successive des pôles et des axes en mouvement au-dessus de l'horizon du Soleil et de leur disparition sous ce même horizon » (5), où les expressions summitas borealis et depressio australis sont relatives au globe solaire, désignant le « pôle Nord » et le «pôle Sud » du Soleil, et nullement les solstices, les apparences résultant éventuellement de cette dernière interprétation ne s'accordant pas avec les observations invoquées par l'auteur.

Bien qu'elles se dissipent généralement sans avoir poursuivi leur trajectoire jusqu'à la circonférence du disque solaire et que leur observation ne puisse, ainsi, se prolonger du bord oriental du disque jusqu'au bord opposé, les taches, emportées par le mouvement général de rotation du globe solaire sur lui-même, doivent être considérées comme décrivant des cercles parallèles au plan de l'équateur solaire. Les traversées du disque par les taches apparaissent donc à l'observateur comme les projections, sur le plan de la base du cône visuel, de sections du globe solaire parallèles à son plan de rotation. La trajectoire réelle d'un point fixe à la surface du Soleil est toujours un cercle issu de la section du globe solaire par un plan parallèle à ce dernier. Ces sections circulaires sont, ainsi, toutes, parallèles entre elles, le cercle de plus grand rayon étant la section du globe par le plan passant par son centre, c'est-à-dire l'équateur solaire, et leur rayon diminuant à mesure que la section est plus éloignée de ce centre.

Les lois de l'optique, s'appliquant à la projection des sections parallèles sur un plan de projection orthogonal à l'axe du cône visuel, aboutissent à une mise en perspective où les sections circulaires sont représentées, aux yeux de l'observateur, tantôt, comme des droites, tantôt, comme des demi-ellipses plus ou moins ouvertes, selon l'angle formé par l'axe du cône visuel avec un plan défini par l'axe de rotation du Soleil et l'axe de l'écliptique. Or, l'axe du cône visuel de l'observateur terrestre, en négligeant la parallaxe horizontale ou en supposant l'observateur au centre du globe terrestre, est dans le plan de l'écliptique. Le plan sur lequel se projettent les sections circulaires est, dès lors, un plan passant par le centre du globe solaire, orthogonalement au plan de l'écliptique, et le disque apparent du Soleil est lui-même dans un plan orthogonal à celui de l'écliptique. De ce fait, la vision perçoit toujours des images situées dans un plan orthogonal à celui de l'écliptique, plan qui est celui de la base du cône visuel. Les images sont elles-mêmes les sections de ce plan de projection par les cercles issus, à leur tour, de la section du globe du Soleil par des plans parallèles à son plan de rotation. On conçoit, dès lors, que les figures qui se dessinent sur le plan de projection dépendent de l'angle formé, par ce dernier, avec cet autre plan, lui aussi orthogonal à celui de l'écliptique, mais dont le privilège est d'être le seul plan orthogonal au plan de l'écliptique, qui soit encore orthogonal au plan de rotation du Soleil.

De même qu'on peut tracer, par le centre de la sphère céleste, une infinité de plans, orthogonaux au plan de l'horizon du lieu d'observation, dont la commune intersection sera la verticale du lieu et dont les sections avec la sphère engendreront les cercles de hauteur, puis, une infinité de plans, orthogonaux au plan de l'équateur céleste, dont la commune intersection sera l'axe du monde et dont les sections avec la sphère engendreront les cercles de déclinaison, et qu'il n'y a, cependant, qu'un cercle de la sphère dont le plan soit orthogonal, à la fois, aux plans de l'horizon et de l'équateur, de sorte que ce cercle, appelé méridien, est le seul cercle de hauteur à être cercle de déclinaison, et inversement, de même, parmi l'infinité des plans qu'on peut tracer, par le centre du globe solaire, orthogonalement à son plan de révolution, dont la commune intersection est l'axe de l'écliptique, ou orthogonalement à son plan de rotation, dont la commune intersection est l'axe du Soleil, il n'y a, cependant, qu'un seul plan qui soit, à la fois, orthogonal au plan de révolution et au plan de rotation. Un tel plan est un plan orthogonal au plan de l'écliptique et qui renferme l'axe du Soleil. Il n'y a qu'un seul plan, passant par l'axe du Soleil, qui soit orthogonal au plan de l'écliptique. L'angle formé, par ce plan remarquable, avec le plan de la base du cône visuel de l'observateur terrestre, détermine les figures sous lesquelles le plan de projection, qui est celui de la base du cône visuel, recueille l'image des cercles décrits par les taches solaires dans des plans parallèles au plan de rotation du Soleil.

Les plans des trajectoires des taches sont toujours parallèles au plan de rotation du Soleil. Le plan de la base du cône visuel est toujours orthogonal au plan de révolution du Soleil. Le plan de révolution et le plan de rotation sont inclinés l'un à l'autre de sept degrés et demi. Il est facile de voir qu'il est possible de définir une situation singulière, où la base du cône visuel est dans un plan orthogonal au plan de rotation et où l'angle formé par ces deux plans est nul. Au cours d'une révolution annuelle du Soleil, la base du cône visuel occupe, successivement, l'infinité des plans qu'on peut mener, par le centre du globe solaire, orthogonalement à son plan de révolution. De ce fait, le plan orthogonal au plan de révolution dans lequel se trouve l'axe de rotation, c'est-à-dire l'unique plan orthogonal, à la fois, au plan de révolution et au plan de rotation, ne se confond pas, en règle générale, avec le plan de la base du cône visuel. C'est uniquement lorsque l'axe du cône visuel, c'est-à dire la droite ménée, en négligeant la parallaxe horizontale, du centre de la Terre, au centre du Soleil, vient rencontrer, à angles droits, le premier de ces deux plans, que la base du cône visuel sera effectivement dans le plan mené, par l'axe du Soleil, orthogonalement au plan de l'écliptique, et que les deux plans : celui de la base du cône visuel, et celui qui est orthogonal, à la fois, aux plans de révolution et de rotation du Soleil, se confondent géométriquement.

Considérons que ce plan, qui était simplement remarquable par sa propriété d'être le seul plan à la fois orthogonal aux plans de révolution et de rotation du Soleil, devient singulier, lorsqu'il se confond, parmi l'infinité des plans qu'on peut tracer, par le centre du globe solaire, orthogonalement au plan de révolution, avec le seul que vient rencontrer à angles droits, pour deux longitudes annuelles du Soleil, l'axe du cône visuel de l'observateur terrestre. Ces deux longitudes, approximativement de 75°et de 255°, sont celles des lieux du Soleil lorsqu'il occupe les points d'intersection des sections de la sphère céleste par ses deux plans de révolution et de rotation. Inversement, il est possible de définir deux autres longitudes remarquables (165° et 345°) pour lesquelles le plan que nous appelions simplement remarquable passe par le centre des moyens mouvements solaires. En corrigeant, cette fois, l'équation, l'axe du cône visuel sera dans le plan remarquable et le plan de la base du cône coupera ce dernier sous un angle droit (6). On comprend, dès lors, comment la figure sous laquelle le plan de projection, dans lequel se trouve la base du cône visuel, recueille l'image de la trajectoire d'une tache solaire, dépend de l'angle formé, par ce plan remarquable, avec le plan de la base du cône.

Pour la commodité de l'exposé, supposons qu'une tache dont on se propose d'étudier la trajectoire soit située sur l'équateur du Soleil. Le mouvement décrit par cette tache se confond donc avec la section du globe solaire par son plan de rotation. Sa trajectoire apparente matérialise, ainsi, l'équateur solaire aux yeux de l'observateur. L'axe de rotation est incliné, au plan de l'écliptique, d'une quantité constante et, tout comme, dans une sphère armillaire, il n'est possible de mener, par l'axe du monde, qu'un seul plan qui soit orthogonal au plan de l'écliptique (plan, dont la section avec la sphère engendre le colure des solstices), il n'est possible de mener, par l'axe de rotation du Soleil, qu'un seul plan orthogonal à celui de l'écliptique. Ce plan est celui dans lequel on mesure l'angle de l'inclinaison de l'axe de rotation sur l'écliptique (82°, selon Scheiner). Il en résulte que, si l'axe de rotation demeure incliné, au plan de l'écliptique, non seulement d'une quantité constante, mais encore vers le même côté (si, donc, on se refuse à attribuer à cet axe un mouvement de précession), ce plan doit demeurer constamment parallèle à lui même au cours d'une rotation du Soleil sur lui-même, l'axe de rotation conservant une direction constante dans les coordonnées écliptiques (soit, approximativement, quinzième degré des Poissons Nord / quinzieme degré de la Vierge Sud). Ce plan, que nous appelions remarquable, passe par le centre des moyens mouvements solaires pour les deux longitudes précédentes, soit, approximativement, 345° et 165°.

Il s'ensuit que, pour les longitudes du Soleil de 75° et de 255°, le plan remarquable, mené par l'axe de rotation, orthogonalement à l'écliptique, se confond avec le plan de la base du cône visuel. Ces deux longitudes, les seules où le Soleil occupe les points d'intersection de ses plans de révolution et de rotation, sont, de ce fait, les seules pour lesquelles la section du globe solaire par son plan de rotation apparaîtra, à l'observateur, sous l'aspect d'une droite, comme fait, toujours, la section de ce globe par son plan de révolution, ces deux droites se coupant sous un angle dont la quantité est égale à celle de l'inclinaison de ces deux plans. Mais, pour toute autre longitude du Soleil, cette section revêt la figure d'une ellipse, dont la plus grande ouverture a lieu pour les longitudes solaires auxquelles le plan remarquable et le plan de la base du cône visuel se rencontrent à angles droits (165° et 345°).

Il en résulte les apparences suivantes. Pour une longitude du Soleil de 75°, la section du globe solaire par le plan de son équateur affectera la figure d'une droite de direction Est-Nord-Est/Ouest-Sud-Ouest (7) ; pour une longitude de 255°, de direction Est-Sud-Est/Ouest-Nord-Ouest (8). Pour une longitude comprise entre 75° et 255°, soit, environ du cinq juin au cinq décembre, elle revêtira l'aspect d'une demi-ellipse, dont la convexité regarde vers le Sud (9) ; pour une longitude comprise entre 255° et 75°, du cinq décembre au cinq juin, vers le Nord (10). Les demi-ellipses atteignent leur plus grande ouverture, correspondant aux longitudes solaires de 165° et de 345°, aux environs du sept septembre (165°) et du cinq mars (345°), où le plan remarquable passe par le centre des moyens mouvements. Les positions caractéristiques des longitudes solaires de 75° et de 255° sont dénommées stationes (statio rectilinea aestiva (75°) (11) ; statio rectilinea hiemalis (255°) (12) ; celles des longitudes de 165° et de 345°, aequilibria ou librationes (aequilibrium, sc. autumnale (165°) (13) ; aequilibrium vernale (345°) (14) ; libratio maxima (15)).

On peut représenter graphiquement les variations apparentes des trajectoires des taches en retenant, par exemple, huit cas caractéristiques. Chacun correspond à une variation de 45° de la longitude du Soleil. Quatre d'entre eux sont les stationes et aequilibria précédents. Pour les longitudes de 30° (vingt avril, courbure convexe dirigée vers le Nord (16) et de 120° (vingt juillet, courbure convexe dirigée vers le Sud (17)),le petit axe de la demi-ellipse a une direction Nord-Nord-Ouest/ Sud-Sud-Est ; pour celles de 210° (vingt octobre; courbure convexe vers le Sud (18)) et de 300° (vingt janvier ; courbure convexe vers le Nord (19)), une direction Nord-Nord-Est/Sud-Sud-Ouest. On peut résumer ces apparences en disant que l'axe de rotation du Soleil semble décrire, avec une période annuelle, un cône ayant, pour sommet, le centre du globe solaire et, pour axe, une droite menée par ce centre, orthogona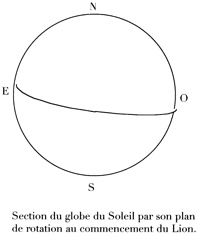lement au plan de l'écliptique.

Dans ces considérations, parfaitement thématisées par les auteurs que nous venons d'examiner, mais entièrement conduites dans les termes d'une astronomie optique, à la manière de Maurolycus et de Ad Vitellionem Paralipomena, se lit, peut-être, l'un des points de départ d'une évolution qui va conduire la pensée, d'un dualisme de l'optique et du physique, caractéristique d'une pensée comme celle de Vitellion, à celui du sensible et de l'empirique, caractéristique d'une pensée comme celle de Kant (20). Nous tenons pour significatif le mode sur lequel la constitution d'une image est pensée à partir des relations, variables, qu'entretiennent deux systèmes de coordonnées, celui des coordonnées physiques, définies dans le cadre de lois géométriques indépendantes du regard de l'observateur ( « Par l'axe de rotation du Soleil, il n'est posssible de mener qu'un seul plan qui soit orthogonal à l'écliptique ») et donnant lieu à la mise en place d'un tissu de relations empiriques ; celui des coordonnées optiques, destinées à prendre en compte les effets de perspective issus de l'appréhension, par le sensible, de ces relations empiriques premières, en fonction de l'angle d'incidence, sur le plan remarquable, de l'axe du cône visuel. Or, le sort de la perspective, comme mode d'articulation du sensible et de l'empirique, se joue dans les ambiguïtés avec lesquelles l'époque répartit les compétences entre optique et physique.

(1) « Quo sane loco mirabile est, semitas Macularum, existente Sole in aequinoctialibus punctis, quasi rectas lineas in disco illius describi ; in cæteris, ac potissimum in Tropicis, curvas ; neque id posse commodius salvari, quam ex eo, quod Sole super eisdem suis Eclipticaeve Polis semper revoluto devehenteque Maculas, Terra se illi ita sistat, nunc, quasi ad dextram sinistramve in aequinoctiis, nunc, quasi sursum deorsumve in solstitiis, ut, propter expositam axis sui continentiam, Maculas videat, non uno modo per discum Solis procedentes, sed cum varietate rectitudinis, curvatisque, memorata. » (Gassendi, De Motu impresso a motore translato Epistulae II, Paris, 1642 ; B. N., R.3538 ; Epistula secunda, p. 148-149).

(2) « Maximum vero circulum Solaris corporis secundum quem, & parallelos eius, fit haec vertigo, ita inclinari ad Eclipticam, ut Macularum motus apparens, in Aequinoctiis, rectas, extra Aequinoctia, curvas lineas describere videatur, sensit Gassendus ; cum, e contrario, Scheinerus dicat eas, prope Solstitia, rectas, in Aequinoctiis & alibi, curvas describere, id vero oriri ab alio quodam motu annuo praeter menstruum, quo poli motus menstrui cum suo axe moventur sensim. » (Riccioli, Almagestum Novum, Bologna, 1651, p. 98, col. 2).

(3) Edizione nazionale, t. V, p. 189.

(4) « Neque id posse commodius salvari, quam ex eo, quod, Sole super eisdem suis, Eclipticaeve, Polis semper revoluto devehenteque Maculas, Terra se illi ita sistat, nunc, quasi ad dextram sinistramve in aequinoctiis, nunc, quasi sursum deorsumve in solstitiis, ut, propter expositam axis sui continentiam, Maculas videat non uno modo per discum Solis procedentes, sed cum varietate rectitudinis curvatisque memorata. » (Gassendi, loc. cit.).

(5) « quo fit ut Sol circa summitatem borealem, & depressionem australem, versus terram annuat sex mensium tempore, & abnuat ab eadem, vicissitudinaria polorum & axium mobilium apparitione supra horizontem solarem, & occultatione infra eundem » (Scheiner, Rosa Ursina, Rome, 1626-1630, p. 601).

(6) On comprend que l'axe de rotation du Soleil est dans le même plan que l'axe du cône visuel. Ce plan est, évidemment, orthogonal au plan de l'écliptique.

(7) « Statio aestivalis rectilinea » (Scheiner, Rosa Ursina, p. 161, col. 2) ; « ex ortu Boreali ad occasum Australem » (Riccioli, Almagestum Novum, III, 3, 8 ; p. 97, col. 1) ; « Circa initium Decembris Iuniique videtur rectilinea. » (ibid.).

(8) « Statio hyemalis rectilinea » (Scheiner, op. cit., p. 162, col. 1) ; « Quae Brumali apparent tempore ex ortivo Austro tendunt ad occasum Boreum » (Riccioli, op. cit., p. 97, col. 1 ; traduction : « Celles qui se présentent en temps d'hiver vont de l'Auster oriental au Borée occidental. ») ; « Hoc iter instituitur, vel motu recto, vel curvilineo. Recto, bis dumtaxat in anno, atque primum quidem sub initium Decembris, ubi Maculae situ recto Solem perambulant. » (Hevelius, Selenographia, Danzig, 1647, p. 90 ; traduction : « Leur trajectoire s'accomplit, soit, d'un mouvement droit, soit, d'un mouvement en ligne courbe. Droit, savoir, deux fois par an, et ce, une première fois, vers le début de Décembre, où les Taches parcourent le Soleil suivant une disposition droite. »).

(9) « At a Geminis in Scorpium, polo eodem avertente se a terra, apparet via illarum curva deorsum versus. » (Riccioli, op. cit., p. 97, col. 1. Traduction : « En revanche, depuis les Gémeaux jusqu'au Scorpion, ce même pôle se détournant de la terre, leur route se présente comme incurvée en direction du bas. ») ; « Per alios sex a Geminis ad Aquarium (lege : Sagittarium), polo inferiore averso convertitur ad nos Superior, omnibus Macularum cursibus deorsum versus curvatis. » (Zucchi, Nova de Machinis Philosophia, Rome, 1649, B. N., V.7205, p. 221 ; traduction : « Tout au long de six autres mois, depuis les Gémeaux jusqu'au Verseau (pour : Sagittaire), le pôle inférieur étant détourné de nous, le Pôle Supérieur est tourné vers nous, toutes les trajectoires des Taches présentant une courbure en direction du bas. » ; ces lignes sont suivies de l'exposition de la libration de la Lune, d'après la Selenographia de Hevelius ; nous avons vu, ailleurs, les conséquences de cette situation) ; « Terra pisces perlustrante, & Sole in (signo Virginis) viso, Polus Boreus maxime nobis tunc attollitur, et Australis latet : planumque maximi circuli, seu Aequinoctialis corporis Solaris, infra planum orbis annui deprimitur : propterea convexitatem motus macularum, ad inferiorem Solis partem vergere ostendit, concavitatem vero centrum respicere, ut pag. 90. adnotasti evenire. » (Boulliau à Hevelius, 11 décembre 1648, B.N., ms. fr. 13.043, fol. 13° v° et ms. fr. nouv. acq. 5.856, fol. 17° v°. Traduction : « Quand la Terre occupe les Poissons, et que le Soleil est vu dans la Vierge, le Pôle Nord est élevé le plus possible à nos yeux, tandis que le Pôle Sud demeure caché et que le plan de son grand cercle, savoir de l'Equateur du corps du Soleil, est abaissé en-deçà du plan de l'orbe annuel ; de ce fait, on voit que la convexité du mouvement des taches est dirigée vers le côté inférieur du Soleil, tandis que sa concavité regarde son centre, comme tu as précisé qu'il arrivait page 90. » Cette dernière référence renvoie, précisément, sous la plume de Boulliau, à la Selenographia de Hevelius.). L'expression « est élevé le plus possible à nos yeux » doit s'entendre au sens de : élevé sur l'horizon, cet « horizon » étant la circonférence apparente du disque du Soleil, la définition la plus générale du terme d'horizon étant un cercle qui partage l'hémisphère visible et l'hémisphère invisible. L'étroite analogie avec la théorie de la Lune et de ses librations mensuelles est clairement perceptible dans ces lignes de Boulliau ; cf. Boulliau à Hevelius, 23 juillet 1655, B. N., mss fr. 13.043, fol. 61 v°- 62 r° : « Certissimum etiam est partes Lunæ boreales aliquando propius margini Lunæ admoveri, aliquando vero minus, eademque proportione australes, illisque ab ora recedentibus accedere, vicissimque illis admotis elongari. Idque pro ratione latitudinis Lunæ, ut recte etiam adnotasti. / Habet equidem motus librationis longitudinis polos suos fixos puncta determinata corporis Lunaris, quod utramque paludem Mæotidem & Maræotidem ab occasu in ortum, respectu orbitæ Lunæ, vicissimque, constantissime ferri videamus, parvaque admodum differentia ipsarum a marginibus distantias variare in librationis terminis. At Poli isti motu etiam librantur motui latitudinis Lunæ etiam commensurabili, ut clarissime ostendit variatio illa phasium limborum Lunæ borealis, et oppositi austrini. Si polus itaque boreus ex hypothesi nobis semper obversus est, quando Luna in limite  boreo fuerit, tunc supra Lunæ hemispærii nobis obversi horizontem minimum attolletur, eritque limbo ad montes hyperboreos vicinissimus. Discedente vero Luna a boreo limite, attollitur polus boreus supra hæmispherium nobis visibile, & a margine boreali recedit. Dixi autem, ex hypothesi, nam fieri potest, ut polus ille boreus semper lateat, vel quandoque abscondatur, quandoque emergat. Ut autem quod sentio dicam, a limbo Lunæ numquam multum distare polos credo, cum linea librationum longitudinis per disci Lunæ centrum fere semper transeat. In eaque sum opinione, polos illos librationis longitudinis in disci horizonte stare, dum Luna in nodis versatur, boreum vero nobis abscondi, Luna a nodo ascendente ad oppositum descendentem currente, australemque cerni. Hunc vero latere, boreumque extare, Luna semicirculum peragrante a nodo descendente ad oppositum. » ; traduction : « Il est également établi avec la plus grande certitude que les parties Nord de la Lune s'approchent, de la bordure de la Lune, tantôt, plus, et, tantôt, moins, et, que, dans la même mesure, les parties Sud, lorsque les précédentes s'écartent du bord, s'en rapprochent et, inversement, lorsqu'elles s'en approchent, s'en éloignent. Et, ce, suivant la raison de la latitude de la Lune, comme, là encore, tu as parfaitement remarqué. / De toute évidence, le mouvement de la libration en longitude a, pour pôles, certains points fixes du corps de la Lune, puisque nous constatons que la Palus Mæotis et la Palus Maræotis se déplacent, toutes les deux, de l'occident vers l'orient, dans le sens de l'orbite de la Lune, et inversement, d'une manière parfaitement régulière et que leur distance à la bordure ne subit, pour les plus grandes valeurs de la libration, qu'une modification extrêmement limitée. Toutefois, ces pôles présentent aussi un mouvement de libration, proportionnel, lui, au mouvement de la Lune en latitude, ainsi que démontre très clairement la modification que subit, sous forme de phases, le bord Nord de la Lune, ainsi que le bord Sud qui lui est contraire. En admettant, donc, par hypothèse, que le pôle Nord soit constamment tourné vers nous, dans ce cas, chaque fois que la Lune sera dans sa limite Nord, il sera, en cette occasion, soulevé le moins possible au-dessus de l'horizon qui circonscrit l'hémisphère tourné vers nous et il sera le plus près possible du bord du côté des Montes Hyperborei. En revanche, lorsque la Lune s'éloigne de sa limite Nord, le pôle Nord s'élève au-dessus de l'hémisphère qui se présente à nous et s'écarte de la bordure Nord. Je dis bien, par hypothèse, car il pourrait se faire que ce pôle Nord demeure constamment caché, ou, encore, que, tantôt, il se dérobe et, tantôt, apparaisse. Mais, pour dire ce que je crois vraiment, je pense que les pôles ne sont jamais à une grande distance du bord de la Lune, puisque la ligne des librations en longitude passe presque constamment par le centre du disque de la Lune. Et telle est mon opinion, que ces pôles de la libration en longitude sont placés dans l'horizon du disque, lorsque la Lune se rencontre dans les nœuds, que le pôle Nord se dérobe à nous, lorsque la Lune passe, du nœud ascendant, au nœud descendant qui lui est contraire, cependant qu'est visible le pôle Sud. Ce dernier, dis-je, demeure caché, cependant que se montre le pôle Nord, le temps que la Lune parcourt le demi-cercle qui sépare le nœud descendant du nœud contraire. ». Nous avons développé, ailleurs, les réflexions que nous inspire le parallélisme entre les théories du Soleil et de la Lune.

(10) « Maculae ex illo motu rectilineo hyberno semper abiverunt in curvilineum eumque fecerunt semper concavum versus austrum, convexum versus boreum, idque pers ex continuos menses. » (Scheiner, op. cit., III, 26, p. 225, col. 2, l. 5 sq. ; traduction : « Les taches sont toujours passées, de ce mouvement en ligne droite, pendant l'hiver, à un mouvement suivant une courbe, qu'elles ont toujours rendu concave en direction du Sud, et convexe, en direction du Nord, et ce, pendant six mois de suite sans interruption.» ; l'auteur en conclut, à juste titre, que la parallaxe du Soleil est insensible) ; « A Sagittario ad Taurum inclusive, polo inferiori axis Solaris ad Terram converso, via macularum apparet curva sursum versus in disco Solis. » (Riccioli, op. cit., p. 97, col. 1 ; traduction : « Du Sagittaire au Taureau inclus, le pôle inférieur de l'axe du Soleil étant tourné vers la Terre, la route des taches se présente comme incurvée en direction du haut, rapportée au disque du Soleil. ») ; « Sol axem & polos suae convolutionis velut menstruae (non enim 27. dies implet) per circulum annuum quasi illi in oppositum inflectit ; ut per sex circiter menses a Sagittario ad Taurum inclusive polus inferior ad Terram convertatur, omnibus Macularum cursibus apparentibus in facie Solis sursum curvatis.» (Zucchi, op. cit., p. 221 ; traduction : « Le Soleil déporte l'axe et les pôles sur lesquels il tourne presque en un mois (cette révolution, en effet, n'occupe pas entièrement 27 jours), au cours de son cercle annuel, quasiment en sens opposé à ce dernier, de telle sorte que, pendant six mois de suite environ, du Sagittaire au Taureau inclus, son pôle inférieur est tourné vers la Terre, toutes les trajectoires des Taches se présentant, dans la face du Soleil, comme incurvées vers le haut. » ; nous avons relevé par des italiques un membre de phrase qui nous paraît décisif pour notre critique de Gassendi ; cf. Descartes, Principes, III, 35) ; « Permeante ergo terra (in Signo Virginis) Sol videtur in (Signo Piscium), & Polus Solis Boreus minimum nobis tunc attollitur, imo latet, & Austrinus nobis obversus est : planumque maximi circuli, seu Aequinoctialis corporis Solis, elevatum supra planum Zodiaci, viam macularum ostendit convexam versus partem superiorem Solis, concavam versus centrum. » (Boulliau à Hevelius, lettre citée du 11 décembre 1648 ; voir à la note précédente pour la référence ; traduction : « Ainsi, la terre demeurant dans la Vierge, le Soleil est vu dans les Poissons, et c'est alors que le Pôle Boréal du Soleil est, à nos yeux, le moins élevé, voire, il est caché, tandis que le Pôle Austral est tourné vers nous ; et le plan de son grand cercle, soit, de l'Equateur du corps du Soleil, élevé au-dessus du plan du Zodiaque, représente la route des taches comme convexe à l'égard du côté supérieur de Soleil, et comme concave, à l'égard de son centre. ») ; « Si cursus hi rectilinei a rectitudine nonnihil deflectere videntur, si versus principium Maii procurrant, sunt, in parte australi, convexi ad centrum C, in boreali, concavi ; contra si fini Iunii propiores existant, fiunt, in parte borea, convexi, in australi, vel concavi vel rectilinei. » (Scheiner, op. cit., p. 225, col. 1, l. 14-21. Traduction : « Si ces trajectoires en ligne droite paraissent s'écarter nettement d'une ligne droite, si elles se produisaient aux alentours du début mai, elles sont, dans l'hémisphère Sud, convexes à l'égard du centre C, et, dans l'hémisphère Nord, concaves ; si, en revanche, elles arrivaient plus près de la fin juin, elles se font, dans l'hémisphère Nord, convexes, et, dans l'hémisphère Sud, soit, concaves, soit en ligne droite. »).

(11) « Statio aestivalis rectilinea » (Scheiner, op. cit., p. 161, col. 2).

(12) « Statio hyemalis rectilinea » (Scheiner, op. cit., p. 162, col. 1).

(13) « Aequilibrium autumnale » (Scheiner, op. cit., p. 161, col. 2, l. 52). « Exinde sequitur aequilibrium autumnale. » (Hevelius, op. cit., p. 90).

(14) « Æquilibrium vernum » (Scheiner, op. cit., p. 162, col. 2) ; « Postea contingit earum aequilibrium vernale, ubi aequali distantia, ad Eclipticam inclinata, Euro & Zephyro absunt : hoc enim nullo alio fit tempore. » (Hevelius, op. cit., p. 90).

(15) « i quali libramenti » (Galilée, Dialogo, Terza Giornata, Edizione Nazionale, t. VII, p. 375) ; « nel giorno della librazione » (ibid.) ; « librationem » (Scheiner, op. cit., p. 601, col. 1, l. 26). Ces expressions doivent s'entendre au sens du Pseudo-Thabit. Le premier auteur à avoir appliqué au Soleil ce vocabulaire que le Pseudo-Thabit et ses successeurs alphonsins (dont l'usage est à l'origine de celui de Copernic) appliquaient à la huitième sphère semble avoir été Scheiner, dont Galilée semble avoir suivi l'usage. Il est remarquable que la traduction latine du Dialogo reprenne le même vocabulaire, e. g. : « tantum per duos totius anni dies erunt hi termini ortuum & occasuum in aequilibrio constituti : post quae libramenta paullatim (sic) incipit inclinatio transitus Macularum, & de die in diem augetur, donec tribus mensibus ad summam obliquitatem perveniat : ex quo loco diminui rursus incipiens, per tantundem temporis ad alterum aequilibrium revertetur. Accidet & quartum hoc admirabile, quod dies maximae obliquitatis is ipse erit, qui & transitus facti per lineam rectam : & in die librationis apparebit arcus transitus plus quam unquam incurvatus. In aliis postea temporibus, pro ut pendentia diminuetur, ac versus aequilibrium tendet, incurvatio arcuum transituum e contrario increscet. » (Dialogus de Systemate Mundi, Augustae Trebidoc. (sic, videlicet forsitan : Strasbourg ??), 1635, B. N., R.3174, p. 339-340 ; traduction : « ...et, pendant deux jours seulement dans toute l'année, ces termini des levers et des couchers auront été posés en équilibre : après ces libramenta, commence, petit à petit, l'inclinaison de la traversée des Taches, et elle s'accuse de jour en jour, jusqu'à ce qu'en trois mois elle arrive à la plus grande obliquité : et, à partir de cette position, commençant, inversement, à décroître, elle reviendra, pendant la même quantité de temps, à son second équilibre. Se produira encore une quatrième conséquence étonnante que voici, le fait que le jour de la plus grande obliquité sera celui-là même qui est aussi celui de la traversée accomplie en ligne droite : et, le jour de la libration, l'arc de la traversée se présentera plus incurvé que jamais. Ensuite, aux autres époques, autant son penchant diminuera et tendra vers l'équilibre, l'incurvation des arcs des traversées, au contraire, augmentera. ».). Signalons ce qui nous apparaît comme une erreur du traducteur latin : « in aliis postea temporibus », où postea n'est pas, d'après le contexte, un adverbe de temps, mais a un sens phraséologique : « ne gli altri tempi poi », cf. le texte italien, à la p. 375. Ce vocabulaire est aussi celui de Copernic lorsqu'il parle de la précession des équinoxes : « Quam ob causam, binos omnino polorum motus reciprocos pendentibus similes librationibus oportet intellegi, quoniam poli & circuli in sphaera sibi invicem cohaerent & consentiunt. Alius igitur motus erit, qui inclinationem permutat illorum circulorum, polis ita delatis sursum deorsumque circa angulum sectionis. Alius, qui solsticiales aequinoctialesque praecessiones auget & minuit, hinc inde, per transversum facta commotione. Hos autem motus librationes vocamus, eo quod, pendentium instar, sub binis limitibus, per eandem viam, in medio concitatiores fiunt, circa extrema, tardissimi... Differunt etiam suis revolutionibus, quod inaequalitas aequinoctiorum bis restituitur sub una obliquitatis restitutione. » (De Revolutionibus..., Nuremberg, 1543, fac-simile, B. N., 4°V.26.638, fol° 66 r° ; traduction : « De ce fait, il y a lieu d'entendre, en tout, deux mouvements réciproques des pôles, semblables aux librations d'une balance, puisque, dans une sphère, les pôles et les cercles sont fixes et solidaires entre eux. L'un des deux mouvements sera donc celui qui modifie l'inclinaison de ces cercles, les pôles étant ramenés vers le haut et vers le bas selon un angle du plan de section. L'autre, celui qui augmente et diminue les précessions des solstices et des équinoxes, deci delà, le déplacement se faisant dans le sens orthogonal. Or, ces mouvements, nous les appelons librations, pour la raison que, à l'exemple d'une balance, dans deux fois deux limites, ils se font plus rapides, au milieu, et très lents, aux alentours des extrémités... Ils diffèrent encore par leurs périodes, parce que l'inégalité des équinoxes se rétablit deux fois pendant que se rétablit une fois l'obliquité. »). Ce sont, là, les « librationum intricationes », les « enchevêtrements de librations » qu'évoquera Tycho Brahé dans la célèbre lettre à Christophe Rothmann du 24 novembre 1589 (Tychonis Brahe Liber I Epistolarum astronomicarum, commencé d'imprimer à Uraniburg et achevé d'imprimer à Francfort, 1610 ; la lettre occupe les pages 155 à 169 ; l'expression citée se trouve à la page 167). Le vocabulaire, comme la doctrine, de Copernic, comme de Galilée, sont ceux des Alphonsins. En revanche, la présence du mot « pendentia » dans les deux textes semble fortuite, puisqu'il signifie inclinaison (féminin singulier ; « secondo che la pendenza si andrà diminuendo »), dans la traduction latine de Galilée, et balance (neutre pluriel), dans le texte de Copernic. Précisons que lorsque Galilée évoque la « libration » de la Lune, il n'emploie jamais ce mot, mais parle de « titubazione », ou, plus exactement, de « titubatione della Luna », ainsi dans l'importante, mais obscure lettre à Alfonso Antonini du 20 février 1638, numérotée 3.684 dans l'Edizione Nazionale, t. XVII, p. 291-297. Mais l'orthographe « titubazione » ne semble attestée que dans une partie de cette lettre que ne reproduit pas l'Edizione Nazionale et qui ne se trouve, à notre connaissance, que dans l'Edizione Bolognese de 1655, qui reproduit une version plus complète de cette lettre, t. II, p. 54-59, où le vocable apparaît souligné vers la fin de la lettre dans l'orthographe correcte. Le premier à avoir parlé d'une « libration » de la Lune semble être Ismael Boulliau, dans l'Astronomia Philolaïca, Paris, 1645. Il est significatif que cet ouvrage contienne une explication de la précession des équinoxes qui témoigne d'une inspiration alphonsine.

(16) « Et prioribus quidem tribus huius semestris mensibus, id est, Martio, Aprili, Maio, omnes arcus itinerarii erunt concavi in Austrum orientalem, convexi in Aquilonem occidentalem. » (Scheiner, op. cit., p. 161, col. 2, l. 41 sq. Traduction : « Et, sans doute, les trois premiers mois de ce semestre, savoir, en Mars, en Avril et en Mai, les arcs que décrivent les traversées seront, tous, concaves à l'égard de l'Auster oriental (sc. du Sud-Sud-Est), et convexes à l'égard de l'Aquilon occidental (sc. du Nord-Nord-Ouest). ») ; « Subsequentibus mensibus tribus, nempe Martio, Aprili & Maio, ita suum gressum attemperant, ut convexa obliquitas earum ad Corum, cava vero ad Euroaustrum vergat. » (Hevelius, op. cit., p. 90 ; traduction : « Les trois mois suivants, savoir en Mars, en Avril et en Mai, elles infléchissent leur mouvement d'une façon telle que leur obliquité convexe est dirigée vers le Corus, et la concave, vers l'Euroauster. »). Le terme obliquitas désigne, toujours, chez Hevelius, une inclinaison dont l'angle est mesuré dans un plan qui contient l'œil de l'observateur, donc, un plan qui passe par le centre de la Terre et par le centre du Soleil (quelle que soit sa longitude), à la différence de inclinatio, qui désigne une inclinaison dont l'angle est mesuré dans un plan qui se confond, grosso modo, avec le plan du disque solaire, donc orthogonal au plan dans lequel se mesure l'obliquitas. Corus désigne le Nord-Ouest, Eurus, le Sud-Est, Euroauster, le Sud-Sud-Est.).

(17) « Aliis vero tribus posterioribus, post Stationem aestivalem rectilineam, id est Iunio, Iulio, Augusto, convertent itinera Macularum suas concavitates in Septentrionem occiduum, convexitates autem in Austrum orientalem. » (Scheiner, op. cit., p. 161, col. 2 ; traduction : « Et trois autres mois, après la Statio aestivalis rectilinea, savoir, en Juin, en Juillet et en Août, les routes des taches tourneront leur concavité vers le Septentrion occidental, et leur convexité, vers l'Auster oriental. ») ; « Mox obliquum suum cursum contrario modo permutant, ita ut Iunio, Iulio & Augusto mensibus convexitas Notapelioten versus, & concavitas Corum versus tendat. » (Hevelius, op. cit., p. 90 ; traduction : « Ensuite, elles inversent l'obliquité de leur trajectoire en sens contraire, de telle sorte qu'aux mois de Juin, de Juillet et d'Août, sa convexité est dirigée vers le Notapeliotes, et sa concavité, vers le Corus. » ; Notus = Auster = Sud ; Apeliotes = Subsolanus = Est ; Notapeliotes = Sud-Est.

(18) « Contraria hisce evenient, ab Aequilibrio Autumnali, quod contingit semper in fine Augusti atque initio Septembris, usque ad Aequilibrium Vernum, in cuius tribus mensibus, Septembri, Octobri, Novembri, omnes Macularum viae sunt concavae versus Aquilonem borealem, convexae erga Austrum occidentalem... » (Scheiner, op. cit., p. 161, col. 2-p. 162, col. 1 ; traduction : « Les apparences contraires des précédentes se produiront, à partir de l'Æquilibrium Autumnale, qui a toujours lieu à la fin d'Août et au début de Septembre, jusqu'à l'Æquilibrium Vernum, où, trois mois, en Septembre, Octobre et Novembre, les routes des Taches sont, toutes, concaves, en direction de l'Aquilon boréal, et convexes, à l'égard de l'Auster occidental...» ; Aquilo = Nord-Est ; Aquilo borealis = Nord-Nord-Est.) ; « Extremis tribus mensibus, iter Macularum rursus fit reflexum, & convexa pars obliquat Notozephyrum, & cava in Arctapelioten, ita tamen, ut, sub Decembrem, iterum fiat directum. » (Hevelius, op. cit., p. 90 ; traduction : «Les trois derniers mois, le chemin des Taches se met, de nouveau, à pencher ; son côté convexe rencontre, de biais, le Notozephyrus, et son côté concave regarde vers l'Arctapeliotes, d'une façon telle, toutefois, qu'à l'approche de Décembre, il devient, à nouveau, droit.». Zephyrus = Ouest ; Notozephyrus = Sud-Ouest ; Arctapeliotes = Nord-Est.).

(19) « Mensibus autem tribus posterioribus, Decembri, Ianuario, & Februario, postquam Statio hyemalis rectilinea celebrata est, flexus itinerarii sunt cavi in Austrum occiduum, convexi in Septentrionem ortivum. » (Scheiner, op. cit., p. 162, col. 1 ; traduction : « Mais, les trois autres mois, en Décembre, en Janvier et en Février, une fois qu'a eu lieu la Statio hyemalis rectilinea, les courbes qu'elles décrivent sont concaves, à l'égard de l'Auster occiduus, et convexes, à l'égard du Septentrio ortivus. ») ; « Postea iter suum magis magisque flexuosum constituunt, ita ut convexa arcus parte ad Arctapelioten, cava vero ad Notozephyrum inclinent. » (Hevelius, op. cit., p. 90 ; traduction : « Ensuite, elles rendent leur trajectoire de plus en plus courbe, d'une façon telle que, du côté convexe de l'arc, elles penchent vers l'Arctapeliotes, et du côté concave, vers le Notozephyrus. »).

(20) Par sensible, nous entendons les formes transcendantales de la sensibilité, donc, l'espace et le temps ; par empiriques, les intuitions formelles que détermine, au sein de ce continuum, l'application des concepts de l'entendement dans le jugement. La représentation de l'espace, en tant que forme du sens externe, peut être mise en relation avec le plan de projection de l'image (planum imaginarium) dans l'Optique de Kepler, dont l'image, en tant que section du cône visuel par un plan, est une détermination. Dans ce contexte, la proposition vitellonienne, suivant laquelle, dans la vision réfléchie, l'image est la chose vue en un autre lieu que le sien, prend un relief saisissant, puisque l'espace devient, à proprement parler, le lieu où, comme image, la chose est vue en un lieu autre que le sien. Toutefois, on ne saurait pousser bien loin la référence adoptée, ici, à la pensée de Kant. L'image (Bild) qui s'inscrit sur le planum imaginarium est, moins, Darstellung, que trace (Spur) s'inscrivant sur une surface d'enregistrement, ce qui autorise, en revanche, un rapprochement avec la conception freudienne d'un appareil psychique constitué de systèmes où s'inscrivent et se conservent les traces inconscientes de perceptions antérieures (Erinnerungsspuren), ainsi, dans la célèbre Entwurf, dans la lettre à Fliess du 6 décembre 1896, ou dans le Chapitre VII de la Traumdeutung.