Eppure, ruota in se stesssa...

Pour l’étude de la théorie de la libration de Cassini, les sources sont au nombre de quatre :

1° une copie, datée de 1669, du compte-rendu de l’observation de l’éclipse de lune du 26 mai 1668. On sait que cette éclipse a été observée de concert par Jean Picard, à Paris (Porte Montmartre), et par Cassini, à Rome (Palazzo Estense), aux fins de déterminer la différence des longitudes de ces deux villes (5). Cette copie, qui, selon une glose marginale, serait de la main d’Agostino Fabri, connu par des documents conservés à la Biblioteca Universitaria de Bologne, se trouve fol. 69 v° - 70 v° du ms français, nouvelles acquisitions, 5.856 de la Bibliothèque nationale de Paris : «La macchia Caspia era molto vicina al margine, come è stata in tutta questa Lunazione da me osservata in ordine all’apparente Librazione... Lora considero come dipendente dalla complicazione di due moti, uno periodico, con cui la Lune sia portata intorno alla Terra con l’asse, che in corso di questo solo resterebbe sempre parallelo a se stesso, onde dall’istesso punto del firmamento vedrebbesi sempre l’istessa faccia Lunare e dalla Terra apparirebbe volvarsi intorno a se stessa contro l’ordine dei segni mostrando sempre faccie diverse, e da un altro moto di rivoluzione intorno ad un proprio asse inclinato in certa forma all’asse del moto periodico, di periodo uguale al medesimo, e similmente secondo l’ordine dei segni <in virtù del quale> mostrando sempre faccie diverse all’istesso punto del firmamento secondo il medesimo ordine dei segni, ma rispetto alla Terra abolisce l’apparenza del moto contro l’ordine dei segni, che cagionarebbe il semplice moto periodico con l’asse Lunare sempre parallelo a se stesso, se non in quanto questi due moti non convengono nell’asse e nell’inegualità, essendo più inuguale il moto Lunare periodico di quello della rivoluzione intorno al proprio asse, dalle quali discrepanze concepisco che dipenda l’apparenza della librazione Lunare, all’incontro alle stravaganze notate dal dottissimo Evelio, onde non vi sia bisogno di riconoscere come reale questo moto di Librazione della Luna di specie differente dai moti soliti circolari insieme e continui all’istesso asse, che negli altri Pianeti si osservano. Siccome per l’apparente retrogradazione dei Pianeti non è necessaria l’introduzione di un nuovo moto reale, che le respinga indietro, ma basta la complicazione di due moti circolari nell’istessa parte.» (6).

2° Des passages récurrents dans les manuscrits préparés par Cassini en vue d’un traité d’astronomie, dont des copies, ou des débris, constituent les ms B, 4, 1-4 de la Bibliothèque de l’Observatoire de Paris, ainsi que le ms français, nouvelles acquisitions, 5.156 de la Bibliothèque nationale (Principales occurrences de l’exposition de la libration de la Lune : Observatoire, B, 4, 1, fol. 399-414, 548, 608, 973-980 («De la Révolution de la Lune autour de son axe.») ; Bibliothèque Nationale, ms fr., nouvelles acquisitions, 5.156, fol. 11 v° - 12 r° ; ce ms semble reproduire en partie le même texte que l’«Abrégé d’Astronomie» du ms B, 4, 2 de l’Observatoire; par exemple, B, 4, 2, fol. 397-398 = B. N., 5.156, fol. 9 = fol. 31-32 de l’«Abrégé»; cf. Observatoire, ms D, 1, 13, qui contient des documents de Jacques Cassini, ayant servi, plus tard, à la rédaction des Eléments d’Astronomie de 1740, parmi lesquels une version de la théorie de la libration que le rapprochement qui s’y trouve suggéré avec les Theses mathematicae de Optica propugnabuntur a Iacobo Cassini die 10. Augusti 1691 in Collegio Mazarineo..., Paris, 1691, permet, peut-être, de dater de 1691; dans cette liasse, intitulée «In opticarum Theseum supplementum ; quae opticorum instrumentorum ope a patre in Observatorio regio inventa sunt», manquent les feuillets qui paraissent correspondre à la théorie de la libration ; le passage français parallèle a pour titre : «Les decouvertes qui ont este faites à l’observatoire royal avec des Lunetes d’aproche.» ; il n’est pas sans signification que le chapitre intitulé «De la lune» soit précédé d’une exposition des variations apparentes des traversées des taches du Soleil, ce qui souligne l’étroite dépendance de toute cette théorie des conceptions de Scheiner ; on y lit notamment : «On a observé que dans le globe de la lune il y a deux poles opposez, toujours adherans aux mesmes taches, eloignez de 5 degrez des poles de l’orbite de la lune transportez dans son globe. Ces poles sont dans un grand cercle qu’on peut appeller colure de la lune, qui est perpendiculaire à son orbite, et parallele au cercle de sa plus grande latitude. Ce colure, qui, comme le colure de la terre dans la révolution journalière, change de situation dans le disque apparent de la lune par le mouvement qu’elle fait autour de la terre et par lequel elle s’éloigne du cercle de sa latitude, porte les deux poles de la lune, avec les taches adherentes et leur fait faire deux cercles polaires par un mouvement qui, dans le disque apparent, va d’occident en orient, et semble imprimer au pole apparent un mouvement, vers le même costé, ce qui cause la libration en longitude et lorsque ce pole par un tel mouvement est elevé sur le disque apparent de la lune, ou bien qu’il l’est (sic) dans l’hémisphère occulte, les taches qui sont autour du pole s’approchent et s’éloignent du centre apparent faisant une espece de libration en latitude. Mais les taches éloignées des poles ne suivent pas le mouvement du colure vers l’orient, parce qu’elles en ont un autre vers l’occident par lequel elles tournent également au tour de l’axe de la Lune dans une période egale a celle du retour de la lune au cercle de sa plus grande Latitude. Ainsi par le mouvement des taches contraire au mouvement apparent du colure il se fait une compensation du mouvement du mesme colure, dont il en resulte que les taches qui sont dans le disque apparent ne souffrent aucune variation... Et il y a encore quelque petite inégalité qui vient de ce que en differens temps tantost le mouvement egal des taches vers l’occident l’emporte sur le mouvement inégal du colure qui se fait du costé d’orient, et tantost celuy des colures l’emporte sur le mouvement des taches, et la différence entre ces deux mouvements fait une autre espece de libration en longitude.» (feuillets non numérotés, où se repère l’allure alambiquée que revêtiront les expositions ultérieures.)).

3° L’exposition, purement verbale, littéraire si l'on peut dire, dans « De l’Origine et du Progrès de l’Astronomie et de ses rapports avec la navigation. », rédigé en 1687, publié, en 1693, dans le Recueil de diverses observations faites en plusieurs voyages par ordre de sa majesté pour perfectionner l’astronomie et la géographie, avec divers Traitez astronomiques, Paris, 1693, réimprimé dans les Mémoires de Mathématique et de Physique de l’Académie royale des sciences, depuis 1666 jusqu’à 1699, tome VIII, Paris, 1730. La théorie de la libration se trouve, à la page 35, dans le premier recueil, aux pages 42-43, du second. On y lit : «Par l’un de ces mouvemens dont la révolution s’achève en 27 jours & un tiers, la Lune paroît tourner d’orient en occident sur un axe parallèle à celui de son orbite. L’autre mouvement se fait réellement d’occident en orient sur un axe dont les poles sont éloignez de ceux de l’orbite de la Lune transportés dans son globe de sept degrez & demi, & des poles de l’écliptique, de deux degrez & demi.». C’est en pensant à ce texte qu’en 1747, Dortous de Mairan écrira : «Nous examinerons bientôt ce qu’il faut entendre par le premier de ces deux mouvemens contraires, ce que je ne sache pas avoir été expliqué nulle part.» («Recherches sur l’Equilibre de la Lune dans son Orbite.», Mémoires de l’Académie royale des sciences pour l’année 1747, p. 4), ajoutant, p. 14, «Ce mouvement ne peut être que celui qui résulte, par la première définition, du parallélisme perpétuel du diamètre DM...par rapport à un point pris hors de la circulation AR ; car dans ce cas, no 14, & selon l’idée des anciens Astronomes, la circulation doit renfermer une révolution entière de la Lune sur son axe... Aussi M. Cassini qualifie-t-il cette rotation de mouvement apparent et inégal : d’apparent, parce que cette rotation n’a rien de réel que relativement à la Terre, ou à quelqu’autre point pris au dedans de sa circulation, & disparoîtroit si la Lune L ou son diamètre DM étoient vûs du Soleil ou des fixes ; d’inégal, parce que, selon l’hypothèse, il suit toutes les inégalités du mouvement de projection de la Lune dans son orbite.». Citons donc pour simple mémoire infâmante les gloses de Delambre, Montucla et autres derviches tourneurs de tables : «Le mouvement d’occident en orient, dans la partie supérieure (!), paraît se faire en sens contraire dans la partie inférieure, la seule que nous voyions... Il était inutile de parler de deux mouvements contraires ; ils sont les mêmes, comme les mouvemens de Vénus et de Mercure ressemblent à ceux de la Terre. Mercure et Vénus paraissent tourner en sens contraire dans leurs passages sur le Soleil. Il en est de même des taches que nous voyons sur la Lune. Celles que nous ne voyons pas, et qui sont dans l’hémisphère supérieur, tournent d’occident en orient comme toutes les planètes.» (Delambre (Jean-Baptiste), Histoire de l’Astronomie moderne, tome II, p. 734.). Il est facile de justifier Cassini en confrontant le texte de 1693 avec celui des Eléments d’Astronomie de Jacques Cassini, de 1740, où l’on lit, p. 259: «Pendant que les Poles du globe de la Lune font leurs révolutions de l’Occident vers l’Orient, le Colûre de la Lune sur lequel ces Poles sont placés, & qui est représenté en ligne droite lorsque cette Planète est à la distance de 90° de ses nœuds, tourne du même sens, & se transforme en une Ellipse dont la largeur augmente jusqu’à ce que la Lune étant arrivée à son Nœud, il se conforme au bord oriental de cette Planète ; & comme ce Colûre qui est fixe sur la surface de la Lune, passe toûjours par les mêmes Taches, il suit que si la Lune n’avoit aucun mouvement autour de son axe, on verroit ces Taches passer successivement du bord occidental de la Lune à son bord oriental, & revenir aux mêmes endroits après le retour de la Lune à ses Nœuds, ce qui est contraire à ce que nous observons de la Lune, dont on découvre toûjours à peu près la même face & les mêmes Taches. /Il est donc nécessaire pour expliquer cette apparence, de supposer que le globe de la Lune tourne autour de ses Poles, d’un mouvement égal & uniforme de l’Occident vers l’Orient, qui, étant vû de la Terre, paroît être de l’Orient vers l’Occident, au contraire du mouvement apparent du Colûre.» ( à confronter aussi à B. N., mss fr. nouvelles acquisitions 5.156, fol. 11 v°-12 r°.).

4° Le mémoire, imprimé en 1721, « Sur la Libration apparente de la Lune, ou de la Révolution de la Lune autour de son axe. », Mémoires de l’Académie royale des sciences, année 1721, p. 108-126, repris dans Cassini (Jacques), Eléments d’Astronomie, Paris, 1740. Dans sa double version, ce mémoire présente des erreurs surprenantes ; en particulier, les planches qui représentent la Lune telle qu'elle se voit dans les latitudes sont inversées (latitude nord pour latitude sud), sans que l'auteur des légendes semble s'en émouvoir ; on remarque, encore, une similitude troublante entre les constructions proposées pour déterminer la position des accidents lunaires sur le disque de la Lune (point important quand on sait que l'observation des éclipses est utilisée pour la détermination des différences des longitudes terrestres) avec des constructions fournies par la Rosa Ursina de Scheiner pour déterminer les trajectoires des taches solaires. Avec les Cassini, le plagiat n'est jamais loin et l'authenticité de toute cette documentation pourrait soulever mainte discussion. Nous-même ne savons quelle est l'origine des recueils de la Bibliothèque Nationale ; peut-être sont-ils constitués de documents soustraits par Libri à la Bibliothèque de l'Observatoire.

«Le mouvement de la Lune autour de la Terre en 27 jours qui fait le mesme effet que feroit le mouvement de la Terre autour de la Lune... » (7). Ce membre de phrase, qui ouvre le chapitre intitulé «De l’apparence de la Libration de la Lune à la Terre», dans le Traité manuscrit d’astronomie attribué à Cassini, nous porte au cœur d'un problème. Nous ne sachions pas que personne ait jamais soutenu l'idée selon laquelle la révolution de la Terre autour de la Lune eût engendré des apparences différentes de celles qui résultent d'une révolution de la Lune autour de la Terre. Mais nous connaissons quelqu'un qui a soutenu, en toute lucidité, qu'une révolution du Soleil autour de la Terre eût engendré des apparences différentes de celles qui résultent d'une révolution de la Terre autour du Soleil. Sentite dunque l'alta e nuova maraviglia.

Fu il primo scopritore ed osservatore delle macchie solari, si come di tutte l'altre novità celesti, il nostro Academico Linceo ; e queste scopers'egli l'anno 1610, trovandosi ancora alla lettura delle Matematiche nello Studio di Padova, e quivi ed in Venezia ne parlo con diversi, de i quali alcuni vivono ancora : ed un anno dopo le fece vedere in Roma a molti Signori, come egli asserisce nella prima delle sue Lettere al signor Marco Velsero, Duumviro d'Augusta. Esso fu il primo che, contro alle opinioni de i troppo timidi troppo gelosi dell'inalterabilità del cielo, affermo tali macchie esser materie che in tempi brevi si producevano e si dissolvevano ; che, quanto al luogo, erano contigue al corpo del Sole, e che intorno a quello si rigiravano, o vero, portate dall'istesso globo solare, che in se stesso circa il proprio centro nello spazio quasi di un mese si rivolgesse, finivano loro conversioni : il qual moto giudico sul principio farsi dal Sole intorno ad un asse eretto al piano dell'eclittica, atteso che gli archi descritti da esse macchie sopra il disco del Sole apparivano all'occhio nostro linee rette ed al piano dell'eclittica parallele... sin che incontratosi meco, doppo alcuni anni, essendo noi nella mia villa delle Selve, in una delle solari macchie solitaria, assai grande e densa, invitato anco da una chiarissima e continuata serenità di cielo, si fecero a mia richiesta osservazioni di tutto il transito di quella, appuntando diligentemente sopra la carta i luoghi di giorno in giorno, nell'ora che il Sole si trovava nel meridiano, ed accortici come il viaggio suo non era altrimenti per linea retta, ma alquanto incurvata, venimmo in pensiero di fare altre osservazioni di tempo in tempo : alla quale impresa gagliardamente ci stimulo un concetto che repentinamente casco in mente all'ospite mio, e con tali parole mel conferi : «Filippo, a gran conseguenza mi par che ci si apra la strada. Imperocché, se l'asse intorno al quale si rivolge il Sole non è eretto perpendicolarmente al piano dell'eclittica, ma sopra di quello è inclinato, come il pur ora osservato passaggio incurvato mi accenna, tal coniettura avremo degli stati del Sole e della Terra, quale né si ferma né si concludente da verun altro rincontro non ne è sin qui stata somministrata». Résumons les pages qui suivent et que chacun peut lire par lui-même. Le rayon visuel d'un observateur terrestre est dans le plan de l'écliptique, ou parallèle à l'écliptique. Le Soleil est vu comme un disque, c'est-à-dire qu'il est vu dans un plan qui est orthogonal au plan de l'écliptique. Le Soleil tourne sur lui-même, en vingt-sept jours, de l'occident vers l'orient, dans un plan qui est incliné au plan de l'écliptique de deux degrés et demi. L'axe de la rotation du Soleil conserve une direction constante, en ce sens que chacun de ses pôles correspond, toujours, à la direction d'un même point de la sphère des étoiles fixes : il quale asse fisso ed immutabile si mantenga perpetuamente nella medesima inclinazione e direzione verso i medesimi punti del firmamento e dell'universo. (8). De ce fait, l'axe de l'écliptique et l'axe de rotation du Soleil définissent un plan remarquable qui demeure, constamment, parallèle à lui-même (Poissons/Vierge). Du fait de l'inclinaison du plan de rotation à l'égard du plan de l'écliptique, le plan dans lequel est vu le disque du Soleil n'est dans le plan remarquable que lorsque le Soleil est dans les Gémeaux ou dans le Sagittaire ; la trajectoire que décrivent les taches solaires, en treize jours, est alors une ligne droite, inclinée, du nord-est, vers le sud-ouest, dans les Gémeaux, ou, du sud-est, au nord-ouest, dans le Sagittaire : segnerebbe sopra la superficie des Sole la circonferenza di quel cerchio che a noi appare una linea retta. Dans les Poissons et dans la Vierge, c'est, au contraire le rayon visuel qui est dans le plan remarquable (il piano del nostro meridiano, nel qual piano sarebbe ancora l'asse della revoluzion del Sole) et la traversée des taches s'accomplit suivant un arc d'ellipse, dont la convexité regarde le nord, dans les Poissons : incurvata col suo convesso verso la parte superiore, et le sud, dans la Vierge : si mostrerà incurvata e col suo convesso verso la parte inferiore. On sait la conséquence que l'auteur en déduit : si c'est la Terre qui se meut autour du Soleil (posta la Terra immobile nel centro dell'eclittica), sarà...necessario dire che l'inclinazion di questo asse non sia fissa e riguardante di continuo verso il medesimo punto dell'universo, anzi che di momento in momento vadia mutando direzione... E' forza dunque dire, tale asse esser convertibile, e talora trovarsi nel piano del cerchio estremo terminator dell'emisferio apparente, allora, dico, quando i passaggi delle macchie appariscono fatti per linee rette e più che mai pendenti, il che accade due volte l'anno ; altre volte poi trovarsi nel piano del meridiano del riguardante, in modo tale che l'uno de' suoi poli caschi nel solare emisferio apparente e l'altro nell'occulto, ed amendue lontani da i punti estremi, o vogliam dire da i poli, d'un altro asse del Sole, il quale sia parallelo all'asse dell'eclittica (il qual secondo asse converrà necessariamente assegnare al globo del Sole), lontani, dico, tanto quanto importa l'inclinazione dell'asse della revoluzione delle macchie... Convien necessariamente porre, l'istesso asse della revoluzione mestrua delle macchie avere una sua propria conversione, per la quale i suoi poli descrivano due cerchi intorno a i poli d'un altro asse, il quale per cio conviene (come ho detto) assegnare al Sole, il semidiametro de i quali cerchi risponda alla quantità dell'inclinazione del medesimo asse ; ed è necessario che il tempo del suo periodo sia d'un anno, avvengaché tale è il tempo nel quale si restituiscono tutte l'apparenze e diversità ne i passaggi delle macchie... Talché, finalmente, per mantener la Terra stabile nel centro, sarà necessario attribuire al Sole due movimenti intorno al proprio centro, sopra due differenti assi, l'uno de i quali finisca la sua conversione in un anno, e l'altro la sua in manco di un mese... Onde quel terzo movimento, il qual si debbe assegnare al globo del Sole in se stesso (non parlo di quello quasi mestruo che conduce le macchie, ma dico dell'altro che deve trasferir l'asse ed i poli di questo mestruo), non si vede ragion nessuna per la quale ei debba finire il suo periodo più tosto in un anno, come dependente dal moto annuo per l'eclittica, che in ventiquatt'ore, come dependente dal moto diurno sopra i poli dell'equinoziale. On sait que ces textes constituent la paraphrase de textes de Scheiner : «Les Pôles sur lesquels tournent les Taches sont au nombre de deux, le Pôle Austral et le Pôle Boréal, opposés l'un à l'autre, et ils sont affectés de mouvements opposés ; et l'un des deux s'avance toujours, la moitié de l'année, dans l'hémisphère apparent du Soleil, l'autre, dans l'hémisphère caché, et celui qui est visible tourne toujours de l'occident vers l'orient, et celui qui est invisible, de l'orient vers l'occident : le pôle austral se lève dans la Statio rectilinea d'Hiver, aux alentours du début du mois de Décembre, époque à laquelle le pôle boréal se couche ; à l'époque de la Statio d'Eté, en revanche, c'est le pôle austral qui se couche, dans la région polaire Sud-Est, aux alentours du début Juin, et que se lève, dans la région Nord-Ouest, le pôle de l'Aquilon ; et c'est ainsi que ces levers et couchers alternés des pôles en Mouvement, qui emportent les axes autour desquels tournent les Taches, prennent toujours une année.» (9). On sait aussi la raison que voyait Scheiner pour que la révolution de l'axe du Soleil devait avoir une période annuelle, plutôt qu'une période diurne : «Le premier est un mouvement local, par lequel le Soleil, tous les vingt-sept jours environ, accomplit une seule révolution sur son propre centre, et, par l'effet de cette conversio, répand avec abondance tout ce qu'il renferme de lumière, tout ce qu'il renferme de virtus radiosa, tour à tour, à la fois sur la terre et sur l'ensemble du ciel et jusque sur chacun des astres en particulier ; et que cette circuitio a été sans doute attachée au Soleil par le Créateur en vue, particulièrement, de la terre, paraît résulter clairement de ce qu'elle n'est pas simple, mais se compose <aussi> d'une circumductio annuelle de l'axe en mouvement, sur lequel s'accomplit le mouvement précédent, ce qui fait que le Soleil, aux alentours de son pôle boréal et de son pôle austral, s'incline vers la terre, le temps de six mois, puis, se relève dans la direction opposée, selon la succession de la visibilité de ses pôles et de ses axes en mouvement au-dessus de l'horizon du Soleil, et de leur occultation en dessous de cet horizon, comme il a été suffisamment démontré à partir de l'observation du Phénomène, en plus d'un endroit, et, particulièrement, dans la Théorie. / Que cette vertiginosa libratio due aux Cercles polaires se fasse donc aussi dans l'intérêt du globe terrestre, ne soulèvera guère, je pense, de controverse parmi les doctes.» (10). On sait encore que l'idée selon laquelle l'axe de rotation d'un globe animé d'un double mouvement, l'un, de révolution, l'autre, de rotation, ne pouvait conserver un habitus constant sans décrire un cône autour de l'axe de révolution a inspiré la conception copernicienne de la précession des équinoxes : «Que les équinoxes et les solstices changent ainsi d'un mouvement inégal, semble être manifeste d'après ce qui précède. De ce phénomène, personne n'indiquera sans doute de cause plus adéquate, qu'une sorte de deflexus de l'axe de la terre et des pôles du cercle équinoxial. Cela, en effet, semble suivre de l'hypothèse du mouvement de la terre. Comme il est manifeste que le cercle qui traverse le milieu des signes demeure constamment sans changement, comme en témoignent les latitudes constantes des étoiles fixes, tandis que l'équinoxial subit un changement. Puisque, si le mouvement de l'axe de la terre s'accordait simplement et exactement avec le mouvement du centre, presqu' aucune avance, comme nous disions, des équinoxes et des solstices ne se présenterait. Seulement, comme ils diffèrent l'un de l'autre, d'une différence, toutefois, inégale, il fut nécessaire que les solstices et les équinoxes, à leur tour, précèdent les lieux des étoiles d'un mouvement inégal. Il se produit la même chose pour le mouvement de déclinaison, qui modifie, à son tour, d'une manière inégale, l'obliquité de l'écliptique, obliquité qu'on ferait mieux, toutefois, d'attribuer à l'équinoxial. De ce fait, il y a lieu d'entendre, en tout, deux mouvements réciproques des pôles, semblables aux librations d'une balance, puisque, dans une sphère, les pôles et les cercles sont fixes et solidaires entre eux. L'un des deux mouvements sera donc celui qui modifie l'inclinaison de ces cercles, les pôles étant ramenés vers le haut et vers le bas selon un angle d<u plan d>e section. L'autre, celui qui augmente et diminue les précessions des solstices et des équinoxes, deci delà, le déplacement se faisant dans le sens orthogonal. Or, ces mouvements, nous les appelons librations, pour la raison que, à l'exemple d'une balance, dans deux fois deux limites, ils se font, plus rapides, au milieu, et très lents, aux alentours des extrémités... Ils diffèrent encore par leurs périodes, parce que l'inégalité des équinoxes se rétablit deux fois pendant que se rétablit une fois l'obliquité.» (11). Il est plus rare qu'on sache que le dénigrement galiléen de Scheiner n'est pas sans rapports avec une remarque de Tycho, au sujet de Copernic, dans une lettre à Rothmann : «Le troisième <mouvement>, une fois supprimé le mouvement annuel, s'évanouit tout seul ; ou, si tu croyais qu'il peut se maintenir en même temps que l'autre, comment, s'il te plaît, pourra-t-il arriver que l'Axe de la Terre tourne dans le sens contraire du mouvement du centre tous les ans, d'une manière si parfaitement concomitante qu'il n'en paraisse pas moins être en repos ? Comment se fait-il encore que son Axe et son Centre soient animés de deux mouvements différents, au sein d'un même corps simple ? Pour ne rien répondre sur ce troisième mouvement, qui se produit en une journée sur son Axe. Je ne dirai pas non plus que l' enchevêtrement des librations, loin de s'accorder au déplacement des Fixes, auquel elles sont destinées, s'en éloigne grandement. Pèse tranquillement ces difficultés et d'autres semblables et, s'il se peut, résous-les dans ton loisir.» (12). Il est encore plus rare qu'on ait entrevu l'étroite relation que la théorie cassinienne de la libration entretient, jusque dans le plus petit détail du choix des vocables ou du degré d'ouverture du compas, avec ces pages de Galilée ou de Scheiner. Celui aux yeux de qui une révolution de la Terre autour de la Lune n'aurait pas produit les mêmes apparences qu'une révolution de la Lune autour de la Terre, c'est, d'une façon aveuglante, celui qui soutenait, en toutes lettres, qu'une révolution du Soleil autour de la Terre n'eût pas produit les mêmes apparences qu'une révolution de la Terre autour du Soleil. Et lorsque Cassini écrit, en 1668, écrit que non vi sia bisogno di riconoscere come reale questo moto di Librazione della Luna di specie differente dai moti soliti circolari insieme e continui all'istesso asse, che negli altri Pianeti si osservano, cette proposition n'est pas séparable d'une proposition selon laquelle non vi bisogna di riconoscere come reale questo moto di Librazione del Sole di specie differente dai moti soliti circolari insieme e continui all'istesso asse, che negli altri Pianeti si osservano. La théorie cassinienne de la libration est la vérité, au sens hegelien, à la fois, de la doctrine de Scheiner et de celle de Galilée. Si Scheiner s'est trompé en affirmant que la conservation de l'habitus de l'axe du Soleil requiert un mouvement annuel, comme s'est trompé Copernic en attribuant un mouvement à l'axe de la Terre, Galilée s'est trompé en disant qu'une révolution du Soleil autour de la Terre produit des apparences différentes de celles que produit une révolution de la Terre autour du Soleil (13).

Dans ces conditions, l'on doit s'interroger sur les raisons qui auraient pu faire que le cas de la Lune fût, au contraire, un cas d'exception. Or, dans les conditions des débuts de l'observation téléscopique, une telle raison n'est pas difficile à trouver. Ce qui fait de la Lune un cas d'exception, c'est, là, encore, quelque chose qui a à voir avec ce qu'on croit être son «axe». Et si nous mettons, à ce mot, des guillemets, c'est parce qu'on a pu entendre, sous ce nom, vers le milieu du dix-septième siècle, des choses assez différentes les unes des autres, et qui ne correspondent que très approximativement à ce que nous croyons être l'axe de la rotation de la Lune. Dans le cas des «autres planètes», l'observation a révélé, depuis 1610, qu'elles accomplissent, généralement, une rotation sur un axe qui semble observer une direction plus ou moins constante à l'égard de la sphère des fixes. Avec une rigueur qui force l'admiration, la question a été posée de savoir si ce modèle peut s'appliquer au cas de la Lune : il s'agit de la première des deux théories du mouvement de la Lune contenues dans l'Astronomia Philolaïca d'Ismael Boulliau (1645).

La première théorie de la libration de la Lune de l'Astronomia Philolaïca admet (a) que «l'» axe du corps lunaire (entendons, une droite menée par le centre du globe lunaire, parallèlement à l'axe de l'orbite lunaire) demeure constamment parallèle à lui-même, i.e. conserve sa direction initiale, au cours d'une révolution draconitique de la Lune ; (b) qu'aux fins d'oblitérer l'apparence, qui devait nécessairement résulter de ces conditions, d'une révolution du globe lunaire sur lui-même, dans le sens rétrograde, soit, rapportée à la face de la Lune tournée vers la Terre, d'occident en orient, la Lune présente une rotation de sens direct, soit, rapportée à la face tournée vers la Terre, d'orient en occident, ayant une période égale à celle de l'apparence qu'elle a pour effet d'oblitérer, soit, la période de la révolution draconitique de la Lune (27 j. et 6h.) (14). L'égalité des périodes la fait rejeter par Boulliau, qui se souvient du sophisme de Salviati dans la Terza Giornata : «Soit LIM, l'écliptique, FEH, la Terre. Soit FH, l'axe sur lequel la Terre accomplit sa révolution en une journée. Soit NOP, l'orbite de la Lune. Supposons que la Lune occupe une position telle, qu'on peut prendre l'un des diamètres de son corps comme étant l'axe BC, dont on demande qu'il conserve une direction parallèle à l'axe de la Terre FH. Il doit nécessairement se produire l'une des deux conséquences suivantes. Ou bien, que la face de la Lune change, ou bien, qu'à chaque révolution périodique, le disque de la Lune tourne sur lui-même de façon à ce qu'elle présente constamment la même face vers la Terre.

Le premier point se démontre comme suit. Lorsque la Lune sera en N, tandis que l'axe BC conservera <sa direction> à l'égard de l'axe FH de la Terre, puisque le corps de la Lune ne tourne pas sur lui-même, seront vues par les habitants de la Terre les parties <B>ASC. En revanche, lorsque la Lune se sera déplacée de N jusqu'à O, tout en conservant, pendant ce temps-là, la direction de son axe BC, alors les parties BASC, qui, lorsque la Lune se trouvait en N, étaient tournées vers la Terre, sont cachées derrière l'opacité de la Lune, cependant que se voient les parties BVDC. Seulement, une semblable apparence ne s'est présentée en aucun endroit. Il y a donc lieu de supposer que, si l'axe de la Lune conserve une direction déterminée à l'égard de l'axe de la terre, la Lune accomplit, autour de ce dernier axe, une révolution de façon à ce que, si le centre de la Lune se déplace en longitude le long du Zodiaque, elle accomplit elle-même une révolution sur son axe en formant des angles égaux en des temps égaux. / Supposons, en effet, que la Lune se trouve, à nouveau, en N et qu'on voie, toujours, ce même hémisphère <B>ASC. Une fois que la Lune sera parvenue en O et aura accompli la moitié d'un cercle, il faut que <B>ASC ait accompli, à son tour, sur l'axe, la moitié d'un cercle et soit parvenu du côté de BVD<C> pour que les mêmes côtés se tournent vers la terre. Or, que les choses se passent ainsi, on aura du mal à le croire quand on sait que la Nature procède toujours par les chemins les plus courts et ne produit jamais un effet grâce à des causes multiples, s'il peut se produire d'une manière simple. / La démonstration aboutira au même, si l'on prenait pour axe de la Lune AD, en lui supposant toujours la même inclinaison à l'égard de l'axe FH de la terre, ou en le supposant parallèle à l'axe EQ. En effet, lorsque la Lune se sera déplacée de N en O, l'axe AD aurait dû, pendant ce temps, se tourner lui aussi vers la terre et le côté ASD, rejoindre le côté AVD pour que les habitants de la terre voient le même visage de la Lune. Seulement, dans ce dernier cas, chose qui va à l'encontre de l'hypothèse, l'inclinaison de l'axe de la Lune AD, à l'égard de l'axe de la terre FH, se trouve changée, puisque, dans le cercle NOP, lorsque l'axe se trouve en O, le point A de l'axe AD a subi une révolution. Pour cette même raison, on ne saurait invoquer la mondre direction constante.» (15).

La seconde théorie de la libration de l'Astronomia Philolaïca consiste à supposer que le globe lunaire est privé de rotation, et qu'en revanche, «l'» axe de la Lune, au sens défini précédemment, au lieu de conserver sa direction initiale et de demeurer constamment parallèle à lui-même, est animé d'un mouvement comparable à la précession de l'axe terrestre, qui lui fait décrire une surface conique «autour» de «l'axe» de l'écliptique (plus exactement, d'une droite menée, par le centre du globe lunaire, perpendiculairement au plan de l'écliptique) en l'espace d'une révolution draconitique de la Lune. Si la Lune ne tourne pas sur elle-même, aux yeux d'un observateur terrestre, c'est toujours, comme pour Kepler ou Galilée, parce qu'elle ne possède pas de rotation, mais si elle présente une libration, c'est en raison de ce mouvement de «son» axe.

C'est dans ces conditions que Boulliau retient la nature physique de la libration. Cette «libration» résultant d'un mouvement par lequel « l' » axe de la Lune engendre une surface conique «autour» de l'axe de l'écliptique, ne saurait être, dans ces textes de 1645, que la libration en latitude. La libration en longitude n'est encore, à cette date, rien d'autre, dans l'esprit de Boulliau, qu'un effet secondaire de la libration en latitude (16). C'est à partir de 1648 seulement que les observations conduiront Boulliau à dissocier la libration en longitude de la libration en latitude (17). Cette dissociation s'appuie sur le fait que la libration en longitude présente une inégalité de huit ans, qui autorise à lui reconnaître une période égale à celle de la révolution anomalistique de la Lune, période de la révolution sidérale augmentée du mouvement mensuel direct des apsides, tandis que la libration en latitude présente une période égale à celle de la révolution draconitique (période de la révolution sidérale, diminuée du mouvement mensuel rétrograde des nœuds). La découverte de l'inégalité des périodes des deux librations a pour effet de «falsifier» la théorie de l'Astronomia philolaïca, qui repose uniquement sur la considération du mouvement supposé de « l' »axe de la Lune. C'est toujours dans ce même contexte que se situent les termes d'une lettre de Boulliau à Alfonso Antonini du 30 juin 1646 (18). Après avoir souligné que la quantité de la parallaxe lunaire ne saurait rendre compte de la libration en longitude (19), Boulliau critique l'idée suivant laquelle «l'»axe de la Lune conserve constamment la même direction en ces termes : «En dehors des parallaxes, il prend aussi en considération le lieu qu'occupe la Lune dans son orbite à elle, orbite qui présente une inclinaison à l'égard de l'écliptique, par l'effet de laquelle, lorsqu'elle accomplit ses révolutions périodiques, elle s'écarte, en latitude, tantôt, vers le Nord, tantôt, vers le Sud. Sur la base de ces fondements, le grand homme formulait une conjecture suivant laquelle la face de la Lune, à l'égard de nous, habitants de la Terre, subirait, jusqu'à un certain point, un changement. Et, cependant qu'il formule ces réflexions, voici qu'il remarque, dans le disque de la Lune, un mouvement d'une façon telle qu'une assez grande tache, qui se trouve à l'ouest, donnerait l'impression, à certains moments, en étant très près du bord occidental, d'effleurer ce dernier, et, au bout de quelques jours, de s'en être éloignée d'une distance telle que, l'espace qui sépare la limite extrême de cette tache du bord de la Lune elle-même, peut contenir la tache tout entière. S'appuyant sur ces données, Galilée se fait fort, en quoi il a parfaitement raison, de pouvoir appréhender le changement qui se produit dans la face de la Lune ; et il dénomme cette modification dans le disque de la Lune «titubation», recourant, ainsi, à un vocable utilisé par les Alphonsins, modification que nous désignons, quant à nous, du terme de libration du corps de la Lune au Livre III de notre Astronomia Philolaïca, Chapitre XIII, où nous faisions également observer que ce très grand homme avait fait allusion, à l'occasion, dans ses Dialogues sur le Système du monde, à cette modification dans la face de la Lune et avait attiré sur elle l'attention du lecteur. Je ne saurais, toutefois, être d'accord avec lui lorsqu'il soutient, dans les Dialogues, que cette libration ou titubation se produit d'une manière telle que la Lune conserve une direction déterminée à l'égard de l'axe de la Terre. Si l'on envisage les choses corrctement, on s'apercevra, en effet, que la face de la Lune ne conserve nullement une direction fixe à l'égard de la terre, dès lors que s'y faufile cette fameuse modification dans le visage de la Lune ; et l'on a l'impression qu'on tombe dans une contradiction, si, une fois admise cette libration, on ajoute, ensuite, cette direction fixe. Sans doute, s'il se conservait toujours une disposition constante et immuable du visage de la Lune, on ne saurait entendre d'autre direction du corps de la Lune à l'égard du corps de la terre que celle par l'effet de laquelle une seule et même quantité de la surface du sol lunaire fût toujours présentée vers la Terre. Je pense, Monsieur, que vous vous rangerez à notre opinion, après avoir observé la Lune au télescope, pendant la durée d'un trimestre. Vous constaterez que cette libration du corps de la Lune accomplit sa révolution en l'espace de vingt-sept jours, plus vingt heures. Il s'agit, là, de celle dont Galilée pensait qu'elle était mensuelle et qu'il a observée comme telle, et c'est la raison pour laquelle on peut facilement conclure qu'il n'y a pas du tout d'équilibre du visage de la Lune aux yeux des habitants de la Terre, sans qu'il y ait, pour autant, de modification globale de la face de la Lune.» (20).

Dernière version de la théorie de Boulliau, dans une lettre à Hevelius, du 23 juillet 1655, accusant réception de l'Epistola de Motu Lunae libratorio :

« Nous reconnaissons, ainsi, qu'est parfaitement exact le résultat que tu as trouvé par une suite ininterrompue d'observations <et> que j'ai également établi par moi-même. A savoir que, lorsqu'<au cours de sa révolution>, la Lune se trouve, une première fois, dans une valeur de son anomalie intermédiaire <entre l'apogée et le périgée>, c'est-à-dire, dans le quartier qui suit l'Apogée dans l'ordre des signes, la Palus Mæotis est très voisine de la circonférence occidentale de la Lune, tandis que la <Palus> Mareotis est à une très grande distance de la circonférence orientale. A l'inverse, <lorsqu'elle se trouve>, une seconde fois, dans une valeur de son anomalie intermédiaire, c'est-à-dire, dans le quartier qui suit le Périgée dans l'ordre des signes, la Palus Mæotis, disions-nous, s'éloigne le plus possible du bord occidental, tandis que la Palus Mareotis se rapproche, le plus près possible, de son bord oriental. En revanche, lorsque la Lune se trouve dans l'Apogée ou dans le Périgée, chacune des deux taches est à une distance moyenne. Que le mouvement de la libration se conforme à cette loi avec une très grande régularité sera évident pour tous ceux qui observeront la Lune par leurs propres moyens et avec leurs propres yeux. Et voilà quelle est la libration du corps de la Lune en longitude, d'occident en orient, et réciproquement. / Il est également établi avec la plus grande certitude que les parties Nord de la Lune s'approchent, de la bordure de la Lune, tantôt, plus, et, tantôt, moins, et, que, dans la même mesure, les parties Sud, lorsque les précédentes s'écartent du bord, s'en rapprochent et, inversement, lorsqu'elles s'en approchent, s'en éloignent. Et, ce, suivant la raison de la latitude de la Lune, comme, là encore, tu as parfaitement remarqué. / De toute évidence, le mouvement de la libration en longitude a, pour pôles, certains points fixes du corps de la Lune, puisque nous constatons que la Palus Mæotis et la Palus Maræotis se déplacent, toutes les deux, de l'occident vers l'orient, dans le sens de l'orbite de la Lune, et inversement, d'une manière parfaitement régulière et que leur distance à la bordure ne subit, pour les plus grandes valeurs de la libration, qu'une modification extrêmement limitée. Toutefois, ces pôles présentent aussi un mouvement de libration, proportionnel, lui, au mouvement de la Lune en latitude, ainsi que démontre très clairement la modification que subit, sous forme de phases, le bord Nord de la Lune, ainsi que le bord Sud qui lui est contraire. En admettant, donc, par hypothèse, que le pôle Nord soit constamment tourné vers nous, dans ce cas, chaque fois que la Lune sera dans sa limite Nord, il sera, en cette occasion, soulevé le moins possible au-dessus de l'horizon qui circonscrit l'hémisphère tourné vers nous et il sera le plus près possible du bord du côté des Montes Hyperborei. En revanche, lorsque la Lune s'éloigne de sa limite Nord, le pôle Nord s'élève au-dessus de l'hémisphère qui se présente à nous et s'écarte de la bordure Nord. Je dis bien, par hypothèse, car il pourrait se faire que ce pôle Nord demeure constamment caché, ou, encore, que, tantôt, il se dérobe et, tantôt, apparaisse. Mais, pour dire ce que je crois vraiment, je pense que les pôles ne sont jamais à une grande distance du bord de la Lune, puisque la ligne des librations en longitude passe presque constamment par le centre du disque de la Lune. Et telle est mon opinion, que ces pôles de la libration en longitude sont placés dans l'horizon du disque, lorsque la Lune se rencontre dans les nœuds, que le pôle Nord se dérobe à nous, lorsque la Lune passe, du nœud ascendant, au nœud descendant qui lui est contraire, cependant qu'est visible le pôle Sud. Ce dernier, dis-je, demeure caché, cependant que se montre le pôle Nord, le temps que la Lune parcourt le demi-cercle qui sépare le nœud descendant du nœud contraire. / (...) Ton hypothèse conduit encore à conclure, sauf erreur, que l'axe de la libration en longitude fait constamment le même angle à l'égard du plan de l'orbis annuus avec le plan de l'orbis annuus et que, par conséquent, il conserve, à son égard, une même direction. Raison pour laquelle l'angle dont le plan de l'orbite de la Lune demeure élevé sur le plan du Zodiaque sera toujours le même que l'angle dont le point G s'écarte du point E, c'est-à-dire, l'angle EBG. (...) Que, par suite, la libration de ces pôles s'accomplisse dans un plan qui demeure constamment le même, en décrivant, donc, une partie de la circonférence d'un grand cercle, cela me semble tout à fait vraisemblable ; dans le cas contraire, en effet, la disposition des taches de la Lune à l'égard du plan de son orbite s'en trouverait grandement changée, chose que nous ne voyons pas se produire. » (21). Cette référence à un plan dans lequel s'accomplit la libration fait évidemment penser au De Motu octavae Sphaerae du Pseudo-Thâbit , chez qui la révolution des équinoxes mobiles autour des équinoxes moyens s'accomplit dans un plan fixe. Toutefois, chez le Pseudo-Thâbit, les équinoxes mobiles décrivent des petits cercles, non des grands cercles, de façon à engendrer, par leurs révolutions, le mouvement dit d'accès et de recès. On peut donc, pour finir, être sensible à cette réminiscence où s'opposent, après tant de siècles, dans le souvenir de Boulliau, les deux modèles principiels dans lesquels l'ancienne astronomie pensait le mouvement de la sphère des fixes, celui de la précession ptoléméenne, et celui de la libration des fixes.

Période anomalistique de la libration en longitude sur un axe perpendiculaire au plan de l'écliptique, soumis, à son tour, à une libration en latitude de période draconitique : ce texte reprend l'essentiel des conclusions de l'Epistola de Motu Lunæ libratorio. La référence à une direction constante de l'axe de la libration en longitude fait problème. L'auteur envisage explicitement cet axe comme possédant des pôles qui sont fixes à la surface du globe lunaire. Or, en 1645, dans l'Astronomia Philolaïca, Boulliau avait cru démontrer l'impossibilité où se trouvait un axe de la Lune, quel qu'il soit, de présenter une direction constante, sans supposer implicitement que la Lune possède une rotation sur son axe, refusée en raison du principe de l'économie des moyens, doctrine renouvelée, en 1646, lors de la rencontre avec Alfonso Antonini. En faisant décrire, à «l'axe» de la Lune, une surface conique dans le plan de l'écliptique, Boulliau se proposait de rendre compte du fait que la Lune présente constamment le même hémisphère vers la Terre, sans tomber dans la supposition d'une rotation de la Lune. On peut donc se demander si la conclusion tirée, ici, de l'Epistola de Motu Lunæ libratorio ne signifie pas que Boulliau regarde désormais cette rotation comme certaine. Mais on n'en trouve aucune trace dans ses écrits ultérieurs et la lettre à Hevelius(!) du 4 mai 1657 réaffirme sans ambages les anciennes positions de l'auteur (22).

Ici, s'arrête l'histoire des théories de la libration de Boulliau. On ne saura peut-être jamais, si Boulliau, dans ses dernières années, a cru, ou non, à une rotation de la Lune.

Pour Boulliau, si l'axe de la Lune conservait sa direction initiale au cours d'une révolution mensuelle de la Lune autour de la Terre, l'observateur terrestre verrait la face cachée de la Lune, à moins de supposer que la Lune tourne sur elle-même avec une période qui devrait, dans cette hypothèse, être égale à celle de la révolution draconitique. Or, écrit-il, c'est, là, quelque chose <quod> vix admittet ille qui Naturam per lineas brevissimas operari noverit et nihil unquam pluribus efficere quae compendio fieri possunt. (23). Boulliau conclut donc que l'axe de la Lune n'occupe pas une position constante au cours d'une révolution mensuelle de la Lune autour de la Terre et qu'il accomplit, de ce fait, une «révolution» mensuelle par laquelle il engendre une surface conique dont l'apex se confond avec le centre du globe lunaire. De ce fait : nous avons, ici, une inférence contraire à celle formulée par Copernic (dans le cas de l'axe de rotation de la Terre au cours d'une révolution annuelle de la Terre autour du Soleil), à celle de Scheiner et de Galilée, ou de Salviati, (dans le cas de l'axe du Soleil au cours d'une révolution annuelle du Soleil autour de la Terre). Pour Copernic, si l'on se fonde sur le cas d'analogie qu'offre sa théorie de la précession des équinoxes, dans laquelle, au cours d'une révolution annuelle de la Terre autour du Soleil, l'axe de rotation de la Terre ne saurait occuper une direction à très peu près constante sans qu'on lui attribue, à cet effet, un mouvement annuel par lequel il engendre une surface conique dont l'apex occupe le centre de la Terre, il n'y aurait, donc, si l'on comprend bien, dans le cas présent de la Lune, aucun mouvement, la direction qu'occuperait son «axe» (sans doute faut-il entendre l'axe de l'orbite de la Lune) correspondrait, au contraire, au cours du mois, pour ainsi dire spontanément, à des points différents sur la sphère des fixes. De même pour Galilée, si l'on se fonde sur les déclarations de Salviati dans la Terza Giornata, d'après lesquelles seul un mouvement, par lequel, en une année, l'axe de rotation du Soleil engendre une surface conique ayant pour apex le centre du Soleil, est susceptible de faire correspondre constamment la direction de cet axe aux mêmes points de la sphère des fixes, conformément aux sources de Galilée dans la Rosa Ursina de Scheiner. Boulliau, en revanche, formule l'inférence inverse : dans la lettre à Hevelius du 11 décembre 1648, il avait critiqué Galilée pour avoir invoqué un mouvement à l'effet de maintenir l'axe du Soleil dans sa position initiale au cours d'une révolution annuelle. Or, contrairement à l'axe du Soleil, l'axe de la Lune présente, dans l'esprit de Boulliau, une direction qui ne correspond pas constamment aux mêmes points de la sphère des fixes au cours d'une révolution mensuelle de la Lune autour de la Terre. Dans ces conditions, de même que, dans le cas du Soleil, il conclut, de ce que la direction de son axe de rotation correspond constamment aux mêmes points de la sphère des fixes au cours d'une révolution annuelle, que cet axe n'a pas de mouvement, il conclut, dans le cas de la Lune, que l'axe de son orbite doit posséder, au contraire, un mouvement, de ce que sa direction ne correspond pas constamment aux mêmes points de la sphère des fixes au cours d'une révolution mensuelle de la Lune autour de la Terre. Les mêmes raisons qui font, dans le cas du Soleil, qu'aux yeux de Boulliau, son axe n'a pas de mouvement, font, dans le cas de la Lune, que son axe présente, au contraire, réellement et physiquement, ce mouvement conique que Boulliau dénonce, à juste titre, aux yeux de la mécanique moderne, dans le cas du Soleil. Là où il y a un mouvement, pour Copernic et pour Galilée, ou, du moins, Salviati, il n'y en a pas pour Boulliau ; inversement, là où il n'y en a pas pour Galilée (24), il y en a pour Boulliau. Là où il y en a pour Copernic, à savoir, dans le cas de l'axe de rotation de la Terre, si, au cours d'une révolution annuelle de la Terre autour du Soleil, cet axe conserve une direction correspondant constamment aux mêmes points de la sphère des fixes. Là où il y en a pour Galilée, à savoir, dans le cas de l'axe de rotation du Soleil, si, dans l'hypothèse d'une révolution annuelle du Soleil autour de la Terre, cet axe conserve une direction correspondant constamment aux mêmes points de la sphère des fixes. Là où il n'y en a pas pour Boulliau, à savoir, au cas où, au cours d'une révolution mensuelle de la Lune autour de la Terre, l'axe de la Lune conserverait une direction correspondant constamment aux mêmes points de la sphère des fixes. Là, au contraire, où il y en a pour Boulliau : au cas où, à l'inverse, l'observateur serait conduit à conclure qu' au cours d'une révolution de la Lune autour de la Terre, l'axe de la Lune ne conserve pas une direction correspondant constamment aux mêmes points de la sphère des fixes. Si, aux yeux de Boulliau, les conditions normales de l'équilibre d'un astre au cours de sa révolution font que son axe conserve une direction correspondant constamment aux mêmes points de la sphère des fixes, le cas de la Lune devient un exemple d'écart à l'équilibre, écart dont doit rendre compte l'hypothèse d'un mouvement physique. Et c'est cette révolution mensuelle de l'axe de la Lune, par l'effet de laquelle cet axe occupe des positions correspondant à des points différents de la surface des fixes, que l'observateur terrestre perçoit, selon Boulliau, comme libration de la Lune.

La libration de la Lune est donc, pour Boulliau, un mouvement physique, par l'effet duquel l'«axe» de la Lune engendre, en un mois, une surface conique autour de l'axe de l'écliptique.

Cette conception de Boulliau est antérieure aux textes de la Selenographia sur les sections du globe lunaire dans les quadratures et est incompatible avec eux. Elle constitue une réaction, non, à la Selenographia, encore moins à l'Epistola de Motu Lunae libratorio, mais, pour l'Astronomia Philolaïca, aux textes galiléens de la Prima Giornata (pour la libration de la Lune), confrontés à une réflexion critique sur la Terza Giornata, et, pour les lettres, à la lettre de Galilée à Alfonso Antonini de 1638.

Modernité des conceptions cinématiques de Boulliau, qui le fait conclure à une incompatibilité de la conservation de la direction de l'axe avec le fait que la Lune présente constamment le même hémisphère vers la Terre. Boulliau est le seul à s'apercevoir de cette difficulté, qui échappe à Kepler, à Galilée et à Hevelius et atteint une forme paroxystique dans les textes de ce dernier, dans la mesure où il s'agit d'observations téléscopiques suivies, ce qui n'est pas le cas de Kepler (l'astronomie de Ad Vitellionem Paralipomena est nettement pré-téléscopique), ni même de Galilée, dont les observations rapportées dans la lettre à Alfonso Antonini n'ont pas la continuité de celles de Hevelius, d'où l'erreur qui consiste à invoquer le mouvement apparent du Mare Crisium (dont la période est mensuelle) comme preuve d'une parallaxe horizontale (dont la période est diurne). Le caractère paroxystique que revêt l'antinomie de la Lune dans les écrits de Hevelius vient de ce qu'ils pensent les observations de la libration dans des concepts proches de ceux de Ad Vitellionem Paralipomena.

         Archaïsme de Boulliau. Refus de la rotation, dont l'hypothèse est, à la fois, formulée, ce qui est moderne, et refusée. Archaïsme d'une libration physique de la Lune, qui rappelle Bruno, suivant la lettre de Copernic.

La Lune ne tourne donc pas sur elle-même ? A ces mots, nous reviennent à la mémoire les paroles d’Aristote : oti oude kulietai ta astra, faneron: to men gar kuliomenon strefesqai anagkh, thj de selhnhj aei dhlon esti to kaloumenon proswpon, commentées par Sir Thomas Heath en ces termes : «It has been commonly remarked that Aristotle draws a curious inference from the fact that the moon has one side always turned to us, namely that the moon does not rotate about its own axis, whereas the inference should be the very opposite. But this is, I think, a somewhat misleading statement of the case and less than juste to Aristotle. What he says is that the moon does not turn round in the sense of rolling along ; and this is clear enough because, if it rolled along a certain path, it would roll once round while describing a length equal to 3,1416 times its diameter, but it manifestly does not do this. But Aristotle does not say that the moon does not rotate ; he does not, it is true, say that it does rotate either, but his hypothesis that it is fixed in a sphere concentric with the earth has the effect of keeping one side of the moon always turned towards us, and therefore incidentally giving it a rotation in the proper period, namely that of its revolution round the earth.» (25).

Nous ne saurions souscrire à cette explication. Outre qu’il est, méthodologiquement, contestable d’attribuer, à un auteur, des sous-entendus, il nous semble qu’au contraire, lorsqu’il refuse, aux astres, la dinhsij, Aristote leur refuse, précisément, la «rotation», à supposer, toutefois, que quoi que ce soit d’approchant, ne fût-ce que lointainement, d’une «rotation», au sens où l’entend Heath, dans le contexte d’une «mécanique» céleste, où s’équilibrent et s’affrontent des forces qui représentent un travail, une certaine dépense d’énergie mécanique, puisse jamais s’être présenté à l’esprit d’Aristote. Les astres relèvent, pour Aristote et ses contemporains, de deux discours possibles, soit, du discours du géomètre, dont la pratique consiste à mesurer, non des forces, mais des mouvements réciproques, pensés dans un concept d’une définition nominale toute galiléenne («Il moto in tanto è moto e come moto opera, in quanto ha relazione a cose che di esso mancano» (26)) et dont, par conséquent, peut servir de critère la perception, soit, du discours du «physicien», entendons, du naturaliste, où peut, sans doute, surgir la question de la nature ou de l’origine d’un mouvement, mais non celle de sa quantité, ni de sa mesure. Or, puisqu’elle reléguait la question de la nature des forces, ou de l’origine du mouvement, et celle de la mesure de sa quantité, dans des branches distinctes, peu communicables, du savoir scientifique, l’ancienne astronomie n’avait, précisément, nulle idée d’une «mécanique» céleste. Nous avons donc à préciser ce qu’entendent, exactement, les Anciens lorsqu’ils disent, si l’on veut, que la Lune «ne tourne pas sur son axe», ou, plus précisément, «qu’elle ne roule pas» (oti ou kulietai), et quelles relations conceptuelles entretient ce « kuliesqai »avec « strefesqai ».

Nous soupçonnons que s’impose, sur ce point, à nous, modernes, une sérieuse mise au point sémantique. Il paraissait naturel à Aristote et à ses contemporains qu’enchâssés en des sphères solides et transparentes qui les entraînaient dans leurs révolutions, les astres présentent toujours une même face vers la Terre. Il paraissait, de même, naturel, aux contemporains de Galilée et de Boulliau, que la Lune présente constamment le même hémisphère vers la Terre. Sans doute, le cercle dans lequel la Lune accomplit sa révolution était excentrique à la Terre, qui n’en occupait pas le centre, et cette excentricité du cercle de la Lune était à l’origine d’une « libration » optique du globe lunaire en longitude, dont nous avons vu Hevelius et Boulliau rattacher, indépendamment, la quantité à celle de l’anomalie de la Lune, tout comme nous avons vu Riccioli regretter, à l’inverse, de ne la pouvoir rattacher à celle de l’excentricité du cercle de la Lune, faute d’avoir dissocié, la libration en longitude, de la libration en latitude. Mais il n’y avait, là, nulle inspiration vraiment nouvelle : le recours aux excentriques, voire aux équants, était, à la fin du moyen âge et à la Renaissance, un procédé courant dans l’astronomie géométrique. La liberté avec laquelle celle-ci disposait de cercles excentriques ou d’équants était l’exact corrélat de l’idée suivant laquelle, en astronomie physique, l’astre ne possédait nul mouvement propre ou inhérent, mais était simplement entraîné par la révolution de la sphère dans laquelle il était serti. L’abandon des sphères solides a pu avoir pour effet, à la fin du seizième siècle, de transférer, physiquement, les mouvements célestes aux corps eux-mêmes, sous la forme de mouvements de révolution ou de translation. Mais le concept de ces mouvements de révolution et de translation ne pouvait toujours pas se penser dans les termes d’une dynamique qui commençait à peine de se constituer. La révolution dans laquelle s’accomplissait la translation de l’astre pouvait, dès lors, retenir de nombreux traits d’un mouvement naturel, circulaire et éternel. Le concept d’inertie n’étant pas dégagé, on n’avait nulle idée d’accélération, ni de force centrifuge. Nous avons beaucoup de difficultés à imaginer, aujourd’hui, qu’on puisse penser la révolution d’un astre autrement que dans les équations différentielles de son mouvement. Cependant, à l’origine, les rénovateurs de l’astronomie géométrique n’étaient pas nécessairement les mêmes que ceux de la dynamique et n’avaient nulle idée d’une mécanique céleste.

Au sein de cette configuration épistémologique instable, appelée à se modifier, à mesure que seront précisées les relations entre géométrie et mécanique, où les concepts de force, d’accélération et d’inertie commencent, à peine, de se dégager, les notions de révolution et de rotation ne sont pas, non plus, nettement distinguées. La mécanique céleste entend, aujourd’hui, par révolution, un mouvement de translation du mobile, par lequel celui-ci occupe, successivement, des points différents, sur une droite, ou sur une courbe, de translation. Mouvement de translation du mobile, la révolution est entièrement distincte, dans son concept, de la rotation, par laquelle un globe tourne sur lui-même. Sous l’effet de la mécanique céleste, nous éprouvons, aujourd’hui, de grandes difficultés à concevoir, comme les auteurs que nous commentons, la révolution d’un astre de manière à lui faire prendre en charge des phénomènes dont l’explication nous paraît revenir, naturellement, au concept de rotation.

Nous voudrions nous appuyer, ici, sur un texte de Dortous de Mairan, qui fait observer qu’on peut concevoir, de deux manières, la révolution d’un corps sphérique (27). Soit, la section de ce corps, par un plan quelconque passant par son centre, coupe la droite de translation, sous des angles toujours égaux entre eux, ainsi que, si la translation se fait selon une courbe, les tangentes menées à celle-ci, en des points successifs, et l’on aura une révolution dite «de glissement» ; soit, au contraire, elle fera, successivement, avec la droite de translation ou avec les tangentes menées à la courbe, tous les angles possibles, et l’on aura une révolution «de roulement» (28).

Les ingénieurs du grand siècle semblent donc avoir entendu, par «glissement», le mouvement de translation d’une roue, d’une boule ou d’un globe, dont un diamètre quelconque, ou la section par un plan quelconque mené par son centre, conserve un angle constant, tantôt, avec l’essieu, tantôt, avec la droite suivant laquelle se déplace le centre de gravité du mobile, tantôt, si le mouvement se fait suivant une courbe, avec les tangentes, en des points successifs, à la ligne de translation. Inversement, on semble avoir entendu, par «roulement», le mouvement de translation, au cours duquel le diamètre ou le plan de section quelconques changent constamment les angles sous lesquels ils coupent l’essieu ou la ligne de translation (29). La question de savoir si, dans ces conditions, le mouvement de la Lune doit être pensé dans le concept d’une révolution «de glissement», ou «de roulement», doit recevoir une réponse complexe. Nous avons vu que les auteurs considèrent que, dans son mouvement, la Lune est en équilibre, si un même diamètre du globe lunaire, ou la section par un même plan mené par son centre, passe constamment par le centre du mouvement moyen lunaire, ou, encore, si, à l’égard de ce centre, un diamètre quelconque du globe, ou sa section par un plan quelconque mené par son centre, conserve des relations constantes, un angle constant ou une inclinaison constante. Il est clair qu’un tel diamètre, ou qu’un tel plan, conserve, dans ces conditions, un angle constant, non seulement à l’égard du centre de l’excentrique, qui est le centre du mouvement moyen, mais encore des tangentes, menées à l’excentrique, en chacun des points qu’occupe, successivement, au cours de sa révolution, le centre de la Lune. Il est non moins clair que, dans ces conditions, la Lune présente, toujours, en gros, le même hémisphère vers le centre du mouvement vrai lunaire, c’est-à-dire vers le centre de la Terre, si ce n’est qu’elle présente, à son égard, une libration optique, dans le plan de sa révolution, dont la quantité sera égale à la différence de l’anomalie moyenne et de l’anomalie vraie, donc, à l’équation, et la période, celle de sa révolution anomalistique. Cette double condition, d’une libration en longitude proportionnelle à l’anomalie, et d’un angle constant sous lequel un diamètre quelconque du globe lunaire rencontre, de ce fait, la droite menée, du centre du globe lunaire, au centre de son mouvement moyen, étant satisfaite par leurs observations, Hevelius et Boulliau concluent, indépendamment, que la Lune «ne tourne pas sur elle-même», entendons que son mouvement doit être pensé dans le concept d’une révolution «de glissement». D’une manière générale, une enquête plus poussée semble confirmer que les contemporains s’accordent à considérer que, dans l’hypothèse d’un excentrique lunaire sans épicycle, la Lune «ne tourne pas sur son axe» (30). Il en va autrement lorsqu’on attribue, à la Lune, un épicycle. Pour qu’un diamètre quelconque du globe lunaire conserve, dans ces nouvelles conditions, un angle constant, avec la droite menée, du centre de l’épicycle, au centre du déférent, il faudra qu’inversement, il fasse, successivement, tous les angles possibles avec la droite menée, du centre du globe lunaire, au centre de l’épicycle. En d’autres termes, pour présenter constamment le même hémisphère vers le centre du déférent, le globe lunaire devra «tourner sur lui-même», avec une période égale à celle de son mouvement en anomalie, entendu, ici, par opposition au mouvement en longitude, au sens de mouvement de l’astre dans l’épicycle, et dans le sens, direct, si l’épicycle est rétrograde, rétrograde, si l’épicycle est direct. La Lune «tournera», donc, «sur elle-même», la différence entre l’anomalie vraie, comptée au centre de la Terre, et l’anomalie moyenne, comptée au centre de l’épicycle, pouvant toujours donner lieu, le cas échéant, à une libration optique en longitude, d’une quantité égale à l’équation (31). La principale difficulté de cette dernière conception réside dans l’obligation d’attribuer, ainsi, au globe lunaire, deux révolutions, de sens contraires, mais de périodes égales. Cette condition d’une égalité des périodes de deux révolutions entièrement indépendantes l’une de l’autre, celle de la Lune, dans l’épicycle, celle du globe lunaire, sur lui-même, répugne autant à la raison que faisait, dans l’esprit de Salviati, celle du mouvement des pôles du Soleil, et de la révolution de cet astre autour de la Terre. Ainsi, un passage de Buridan, cité et traduit par Duhem, remarquable par l’analogie que présente la structure de son argumentation avec celle qu’on trouve, trois siècles plus tard, chez Boulliau, s’appuie sur cette difficulté, pour refuser l’hypothèse de l’épicycle lunaire. Dans la traduction qu'en donne l'historien, ce passage se libelle comme suit : «Il n’est, sachez le bien, qu’une seule échappatoire : elle consiste à dire que, de même que l’épicycle se meut autour de son propre centre, de même le corps de la Lune se meut autour de son centre particulier, en sens contraire du mouvement de l’épicycle, et avec la même vitesse; en sorte que la Lune accomplisse sa révolution dans le temps même où l’épicycle accomplit la sienne.» (32). Le cas de Buridan présente de fortes analogies avec celui de Boulliau. Appliquant, à la révolution de la Lune, dans l’épicycle, l’idée qu’un astre présente, «naturellement», toujours la même face vers le centre du cercle qu’il parcourt, Buridan est conduit, spontanément, à penser cette révolution dans le concept d’une révolution de glissement. De ce fait, un diamètre quelconque du globe lunaire, coupant, sous un angle constant, le rayon vecteur de l’astre, dans l’épicycle, coupera, au contraire, sous des angles variables, le rayon vecteur de l’épicycle, dans le déférent. Dans ces conditions, la Lune présentera, successivement, toutes ses faces au centre du déférent, chose qui répugne à l’expérience. Buridan ne peut oblitérer cette apparence d’une révolution optique de la Lune sur elle-même qu’en invoquant une révolution physique compensatrice, de même période et de sens contraire, chose qui répugne à la raison. Il conclut, donc, que la Lune n’a pas d’épicycle (33). Dans le cas de Boulliau, les conditions sont, sans doute, différentes, mais elles produisent les mêmes effets. Si l'on admet que deux diamètres quelconques du globe de la Lune définissent un plan qui conserve sa position dans un référentiel inertiel, on est amené à introduire une rotation de la Lune dont la période doit être celle de la révolution draconitique. Comme dans le cas de Buridan, c’est l’égalité des périodes de révolution qui conduit Boulliau à refuser ce modèle. Afin d’élider la difficulté que représente, à ses yeux, l’hypothèse de l’égalité des périodes de deux mouvements indépendants l’un de l’autre, Boulliau refuse l’idée qu’il croit avoir été exprimée par Galilée, suivant laquelle un diamètre quelconque du globe lunaire conserve des relations constantes dans un référentiel inertiel.

Quelles que soient les objections plus ou moins sottes qu’on élève à l’encontre de l’idée d’une égalité des périodes de révolution et de rotation, et qu’on verra ressurgir, un siècle plus tard, à propos de la coïncidence des équinoxes de la Lune avec ses noeuds : croyance au hasard («Le hasard ne pourrait jamais faire que...»), ou, à l’inverse, ce qui revient, du reste, au même, à la providence («Seule, la providence pourrait faire que...»), la raison majeure du refus de Boulliau d’envisager, à la fois, la conservation de la direction initiale d’un diamètre quelconque du globe lunaire, et la révolution compensatrice du globe sur lui-même, nous paraît, toutefois, résider dans le cas d’analogie qu’offrent ces dispositions avec la théorie du Soleil chez Scheiner. D’avoir percé à jour le paralogisme qui consistait, chez Scheiner, suivi par Galilée, à attribuer, à l’axe du Soleil, une révolution, dans le sens rétrograde et avec une période égale à celle de la révolution du Soleil autour de la Terre, le fait reculer devant ce qui lui apparaît, dans le cas de la Lune, comme une situation analogue. Mais, en même temps, une pareille position sera à l'origine d'un embarras profond de sa part lorsqu'il recevra, vers la fin de 1654 ou dans les premiers jours de 1655, l'Epistola de Motu Lunae libratorio de Hevelius. Sans doute, pas plus que Boulliau, Hevelius n'admet une révolution de la Lune sur elle-même, mais la doctrine que développe cette lettre conduit à une antinomie insurmontable au sein du champ de représentations où se meut la pensée des contemporains, pour des raisons que Hevelius n'aperçoit guère, mais dont nous croyons percevoir l'écho dans la lettre de Boulliau à Hevelius, datée du 23 juillet 1655, qui constitue sa réponse à l'envoi de l'Epistola de Motu Lunae libratorio. Essayons de restituer l'origine de cette antinomie, dont l'histoire commence, peut-être, dans une remarque de Galilée, dans une lettre à Frà Fulgenzio Micanzio, du sept novembre 1637 (34), relative à ce qu'il appelle la libration annuelle.

La libration annuelle est le troisième des trois librations qu'évoque cette lettre. Ces trois mouvements sont distingués, par Galilée, d’après leurs périodes, diurne, dans le cas de la parallaxe horizontale, mensuelle, dans le second cas, annuelle, dans le troisième : «Queste tre diverse mutazioni hanno tre diversi Periodi, impero che l’una si muta di giorno in giorno, e cosi viene ad avere il suo Periodo diurno ; la seconda si va mutando di mese in mese, ed ha il suo Periodo mestruo ; la terza ha il suo periodo annuo, seconda il quale finisce la sua variazione.». Sans autres précisions, ce troisième mouvement demeure mystérieux, mais il s’éclaire à la lumière des termes de la lettre du vingt février 1638 à Alfonso Antonini : «Scorgerasse anco mutazione circa gli emisferii illuminati dal sole, atteso che il limbo, o vogliam dir taglio, della illuminazione, per altro verso segherà la faccia della luna veduta da noi quando ella si separa dal sole posto vicino ai nodi, e per altro verso si vedrà tal segamento nel suo primo apparire, separandosi dal sole quando ella sia nell’uno o nell’altro ventre : e di tal mutazione potremo dire il periodo essere annuo, essendo il ritorno del sole al medesimo nodo quasi annuo, per la tardità del moto di essi nodi.». Galilée exprime, ici, l’idée que, selon la latitude de la Lune, la section du globe lunaire par le plan de la base du cône d’illumination est diversement inclinée au plan de l’orbite lunaire. Ce fait résulte de ce que la limite de l’hémisphère lunaire éclairé, appelée, ici, taglio, ou segamento, et, chez les modernes, terminateur, correspondant au Circulus illuminationis du Chapitre VI de Ad Vitellionem Paralipomena, est une section du globe lunaire par un plan perpendiculaire au plan de l’écliptique, et que le plan de l’orbite lunaire est incliné à ce dernier de cinq degrés.

Ainsi, lorsque la quadrature se produit dans les nœuds, le terminateur sera incliné, au plan de l’orbite, de 85°, faisant, avec la normale au plan de l’orbite, menée par le centre du globe lunaire, un angle de cinq degrés, dans le plan apparent (35) du disque lunaire, et l’observateur terrestre voit le terminateur, dans le nœud ascendant, dans une direction Nord-Est/Sud-Ouest, et la normale au plan de l’orbite, dans une direction Nord-Ouest/Sud-Est, et, dans le nœud descendant, le terminateur, dans la direction Nord-Ouest/Sud-Est, et la normale au plan de l’orbite, dans la direction Nord-Est/Sud-Ouest. Lorsque la pleine lune se produit dans les plus grandes latitudes, la section du globe lunaire par le plan de la base du cône d’illumination (Circulus illuminationis de Ad Vitellionem Paralipomena, orthogonal au plan de l’écliptique) ne sera pas dans le même plan que la section par le plan de la base du cône visuel (Circulus visionis, orthogonal, en corrigeant la parallaxe horizontale, au plan de l’orbite). Dès lors, l’hémisphère éclairé de la Lune ne coïncide pas avec l’hémisphère visible et le disque lunaire ne sera pas complètement éclairé. Nous pouvons, dès maintenant, conclure qu’un diamètre de la base du cône d’illumination, parallèle à l’axe de l’écliptique, et un diamètre de la base du cône visuel, parallèle à l’axe de l’orbite lunaire, tout en conservant toujours une inclinaison mutuelle de cinq degrés, définissent un plan qui demeure constamment parallèle à lui-même au cours d’une révolution draconitique de la Lune, plan qui passe par le centre de la Terre lorsque la Lune est dans ses plus grandes latitudes et qui coupe à angles droits la ligne des nœuds (36). Ce plan, dont la section avec la sphère céleste engendre un cercle qui passe, à la fois, par les pôles de l’écliptique et par les pôles de l’orbite lunaire et qui se confond avec le cercle de latitude (37) qu’occupe le centre de la Lune dans les plus grandes latitudes, est, ainsi, celui d’une sorte de «colure» (38) de la Lune.

Ces considérations, imparfaitement dégagées, par Galilée, dans la lettre à Alfonso Antonini, rencontrent une remarque de Kepler, suivant laquelle, la Lune ne saurait jamais être pleine, car la base du cône d’illumination et la base du cône de vision ne se rencontrent dans un même plan (39) que dans les nœuds, lorsque la Lune est près de s’éclipser (40). Remarque reprise et confirmée par Hevelius, qui fait observer, dans la Selenographia, que, lorsque la pleine lune n’est pas dans le plan de l’écliptique, le disque lunaire présente une frange obscure, tantôt, au Nord, tantôt, au Sud, proportionnelle à la latitude (41). Lorsque la latitude est boréale, la frange obscure apparaît au Sud ; elle apparaît au Nord, lorsque la latitude est méridionale (42).

Soient EF, la section du globe lunaire par le plan de la base du cône, ou, comme dit Hevelius, de la pyramide, d’illumination, plan orthogonal au plan de l’écliptique, et GH, la section du globe lunaire par le plan de la base du cône, ou de la pyramide, visuels, plan orthogonal au plan de l’orbite lunaire. EF et GH coïncident lorsque la Lune est dans les nœuds, où les deux sections sont dans un seul et même plan (43). Mais, lorsque la Lune est dans la plus grande latitude Nord, le pôle Sud, F, de l’écliptique est à l’intérieur du disque apparent de la Lune, tandis que son pôle Nord, E, est rejeté dans l’hémisphère caché. Or, quelle que soit la phase de la Lune, le terminateur passe par ces points E et F, situés sur la section du globe lunaire par le plan de la base du cône d’illumination. D’autre part, le plan apparent du disque lunaire est toujours, en corrigeant la parallaxe horizontale, orthogonal au plan de l’orbite lunaire. Il en résulte que, si la pleine lune se produit dans la plus grande limite Nord, le disque lunaire présente une frange obscure, correspondant à l’arc de cinq degrés compris entre F et H, vers son bord inférieur ou méridional. A la lunette, le bord supérieur, ou septentrional, du disque offrira l’aspect lisse (laevis) du bord ocidental dans le premier quartier ou du bord oriental dans le dernier quartier ; en revanche, le bord inférieur, ou méridional, aura l’aspect irrégulier (asper) que présente, dans les quadratures, le terminateur (44). La Lune ne saurait donc être vraiment pleine qu’au voisinage des nœuds ; encore faut-il qu’elle ne s’en rapproche pas au point de provoquer une éclipse ; en revanche, lorsque la pleine lune arrive dans la plus grande latitude Nord, elle laissera une frange obscure (scabrosa) vers le Sud. L’inverse arrive dans la plus grande latitude Sud : le pôle Sud de l’écliptique, F, sera dans l’hémisphère caché ; l’aspect du bord du disque sera lisse vers H, et il présentera une frange obscure vers le bord supérieur ou septentrional (45).

Ces phénomènes traduisent une situation où l’axe de l’écliptique et l’axe de l’orbite lunaire demeurent, chacun, parallèles à eux-mêmes et conservent leurs directions initiales, ainsi que leur inclinaison réciproque, lorsque la longitude de la Lune augmente de 180° et qu’elle passe, de ce fait, de sa plus grande latitude Nord, à sa plus grande latitude Sud. Il revient en effet au même de dire qu’au cours d’une révolution draconitique (46) de la Lune, deux droites menées par le centre du globe lunaire, perpendiculairement, l’une, au plan de l’écliptique, l’autre, au plan de l’orbite lunaire, sont dans un plan qui demeure constamment parallèle à lui-même, ou de dire que l’axe de l’écliptique et l’axe de l’orbite lunaire demeurent inclinés l’un à l’autre, d’une quantité constante et dans un plan conservant une direction constante. Cependant, le centre de la Terre et le centre de la Lune étant, tous les deux, dans le plan de l’orbite lunaire, la linea visiva de l’observateur terrestre, c’est-à-dire l’axe du cône visuel, sera, elle aussi, en corrigeant la parallaxe horizontale, dans ce plan. Le circulus visionis sera donc une section du globe lunaire par un plan orthogonal au plan de l’orbite, très peu éloignée, eu égard à la distance qui sépare la Terre de la Lune, d’un grand cercle passant par le centre du globe lunaire. Il en résulte qu’une droite menée par le centre du globe lunaire, perpendiculairement au plan de l’orbite, donc, parallèle à l’axe de l’orbite lunaire, sera, à peu de choses près, dans le plan du circulus visionis. On peut donc considérer, pratiquement, ce dernier comme une section du globe lunaire par un plan, mené par le centre du globe lunaire, perpendiculairement au plan de l’orbite lunaire. Ainsi, la circonférence apparente du disque lunaire est, quasiment, une section du globe lunaire par un plan mené par son centre, perpendiculairement au plan de l’orbite de la Lune, et le plan du disque lunaire est, de toute façon, après correction de la parallaxe horizontale, dans un plan orthogonal au plan de cette orbite. Or, si, conformément à la définition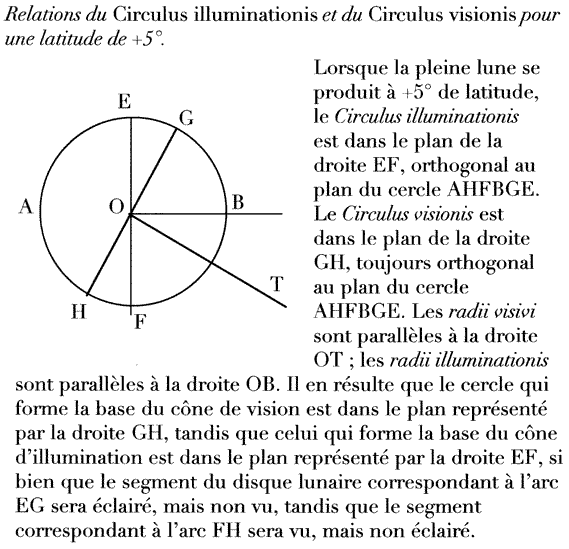 que donnent, de l’image, Ad Vitellionem Paralipomena, l’image est la chose vue en un autre lieu que le sien, le plan dans lequel est vue la Lune est, dès lors, un plan orthogonal au plan de l’orbite lunaire, laquelle fournit, ainsi, les coordonnées dans lesquelles est vue la Lune par l’observateur terrestre, ou coordonnées optiques de la Lune.

Il devient possible, dans ces conditions, d’attribuer, à la Lune, un axe et des pôles particuliers, liés à ces coordonnées optiques. Par l’axe de la Lune, on entendra, en l’occurrence, une droite menée par le centre du globe lunaire, perpendiculairement à son plan de révolution, donc, parallèle à l’axe de l’orbite lunaire (47). Par pôles de la Lune, on entendra les points dans lesquels cette droite rencontre la surface du globe lunaire. Or, nous voyions qu’on pouvait, pratiquement, considérer qu’une telle droite était dans le plan du circulus visionis. Il en résulte que, pratiquement, les pôles propres de la Lune sont situés, non seulement sur la section du globe lunaire par un plan, mené par son centre, perpendiculairement au plan de l’orbite lunaire, mais sur le circulus visionis lui-même, donc, sur la circonférence apparente du disque lunaire.

Or, le circulus illuminationis, complètement indépendant du circulus visionis, puisqu’il dépend des relations que la Lune entretient, non plus avec la Terre, mais avec le Soleil, est une section du globe lunaire par un plan orthogonal, non plus au plan de l’orbite lunaire, mais au plan de l’orbite du Soleil, donc, de l’écliptique. Là encore, mais pour d’autres raisons, le plan orthogonal passe, à très peu près, par le centre du globe lunaire, et la section qu’engendre sa rencontre avec ce globe se confond, pratiquement, avec un grand cercle. On peut, alors, penser à Lagrange qui, en 1764, parlera d’une écliptique lunaire, pour désigner un plan mené par le centre du globe lunaire, parallèlement au plan de l’écliptique (48), et désigner, par axe de l’écliptique lunaire, une droite menée par le centre du globe lunaire, perpendiculairement au plan de l’écliptique, et, par pôles de l’écliptique lunaire, les points dans lesquels cette droite rencontre la surface du globe lunaire.

Dans ces conditions, l’hémisphère lunaire apparent ou visible est circonscrit par une section du globe lunaire par un plan orthogonal au plan de l’orbite lunaire et, les coordonnées mécaniques de ces plans étant les coordonnées optiques de la Lune, ou coordonnées dans lesquelles l’observateur placé au centre de la Terre voit la Lune, les pôles de la Lune, correspondant aux pôles de l’orbite, seront toujours situés, en corrigeant la parallaxe horizontale, sur la circonférence de la base du cône visuel. En revanche, l’hémisphère lunaire éclairé par le Soleil est circonscrit par une section du globe lunaire par un plan orthogonal au plan de l’écliptique (49). Or, en les assimilant à des grands cercles, passant par le centre du globe lunaire, les deux sections ne sont dans un même plan que lorsque la Lune est dans ses noeuds et elles seront décalées, l’une par rapport à l’autre, d’une certaine quantité angulaire, dès que la Lune acquiert une latitude. Dans la pleine lune, l’hémisphère éclairé varie donc selon la latitude de la Lune, cependant que, sans l’intervention de nouveaux facteurs (50), l’hémisphère apparent demeure constamment le même. De ce fait, l’indépendance réciproque de l’orbite lunaire et de l’écliptique, leur inclinaison constante et, dans les limites d’une révolution draconitique, vers le même côté, engendrent un déplacement angulaire apparent du circulus visionis, section du globe lunaire par un plan orthogonal au plan de l’orbite, à l’égard du circulus illuminationis, section du globe lunaire par un plan orthogonal au plan de l’écliptique, se traduisant, dans la pleine lune, par un passage périodique, de l’hémisphère éclairé à l’hémisphère obscur, des parties du sol lunaire voisines des pôles de la Lune et des pôles de l’écliptique lunaire.

Ainsi, cette libration que Galilée qualifiait d’annuelle dépend de l’angle sous lequel l’observateur voit deux droites, parallèles, l’une, à l’axe de l’orbite lunaire, l’autre, à l’axe de l’écliptique, inclinées, l’une à l’autre, d’une quantité constante et, dans la limite du mois draconitique, vers le même côté (ou dans le même plan). La quantité de l’inclinaison réciproque de ces deux droites est égale à celle de l’inclinaison du plan de l’orbite lunaire au plan de l’écliptique, soit, de cinq degrés. En revanche, c’est uniquement lorsque la Lune occupe l’un des nœuds, que l’observateur terrestre verra, effectivement, les deux droites se couper sous un angle de cinq degrés. En effet, lorsque la Lune parvient à l’une des plus grandes latitudes, le plan défini par les deux droites passera aussi par la centre de la Terre (51). Par conséquent, les droites seront vues, depuis la Terre, dans la même direction et paraîtront se superposer et se confondre. D’une façon générale, l’angle sous lequel l’observateur terrestre voit se couper les deux droites varie d’un instant à l’autre sous l’effet du mouvement de la Lune autour de la Terre. Sans doute, feront-elles toujours, «physiquement», un angle de cinq degrés, mais cette inclinaison paraîtra inférieure à l’observateur terrestre pour toute latitude de la Lune différente de zéro degrés. En un sens, c’est, là, l’indice de la nature optique du phénomène, qui dépend, simplement, de l’inclinaison constante des deux plans de l’orbite lunaire et de l’écliptique, mais on peut se demander quel statut doit recevoir, dans une cosmologie comme celle de Hevelius, le plan défini par les deux droites, c’est-à-dire, au fond, par l’axe de l’orbite lunaire et par l’axe de l’écliptique, plan qui demeure constamment parallèle à lui-même au cours d’une révolution draconitique de la Lune. Puisque son mouvement apparent a pour effet de varier l’extension de l’hémisphère éclairé de la Lune, on doit supposer que, dans l’esprit de Hevelius, il coupe toujours la surface du globe lunaire dans les mêmes points, autrement dit, qu’il passe toujours par les mêmes points, matérialisés par des taches ou autres accidents, du sol lunaire, mais on ne voit plus comment, dans ces conditions, la Lune peut encore, en l’absence de nouvelles déterminations, présenter constamment le même hémisphère vers la Terre. Sans doute, ce dernier fait renvoie aux coordonnées optiques de la Lune, donc à un système de coordonnées dont les axes sont fournis par le plan de l’orbite lunaire et sa normale menée par le centre du globe lunaire, mais, puisqu’il passe, à la fois, par l’axe de l’orbite lunaire et par l’axe de l’écliptique, le plan qui demeure parallèle à lui-même au cours de la révolution draconitique présente précisément cette propriété remarquable d’être orthogonal, à la fois, au plan de de l’écliptique et au plan l’orbite lunaire. Or, il ne peut demeurer orthogonal au plan de l’orbite qu’en accomplissant, précisément, une révolution complète, en un mois draconitique, révolution qui traduit le mouvement apparent par lequel l’axe de l’orbite décrit, tous les mois, un cône autour de l’axe de l’écliptique. De ce fait, ce plan remarquable accomplit bien, aux yeux de l’observateur terrestre, une révolution mensuelle sur l’axe de l’écliptique, que la conscience scientifique moderne pourra bien déclarer optique, mais qui n’en devrait pas moins entraîner l’hémisphère visible de la Lune dans son mouvement, ce qui n’est pas le cas.

Ainsi, l’explication que donne Hevelius de la libration que Galilée appelait annuelle soulève bien des difficultés. Dans le cours de la Selenographia, ces difficultés en rencontrent d’autres, liées à la conception que se fait Hevelius du mouvement des taches du Soleil.

Cependant, en 1654, Hevelius publie la première théorie de la libration qui distingue correctement entre libration en longitude et libration en latitude. Il attribue, à la première, la période de la révolution anomalistique de la Lune, et à la seconde, celle de sa révolution draconitique. La distinction de deux librations se fonde sur la reconnaissance que ces deux mouvements ont des périodes distinctes et présentent des inégalités différentes. Hevelius rattache l’inégalité de la libration en longitude, au mouvement des apsides de l’orbite lunaire, et celle de la libration en latitude, à celui des nœuds. La première aura, par conséquent, une période de plus de huit ans, la seconde, de dix-huit ans et sept mois. Cette période anomalistique de la libration en longitude fut découverte, indépendamment, entre 1648 et 1650, par Hevelius et par Boulliau( 52).

Lorsqu’en 1651, parut, à Bologne, l’Almagestum novum de Riccioli, Hevelius y trouva, formulée à l’irréel, l’hypothèse, refusée par l’auteur, suivant laquelle «la» libration vient de l’excentricité du cercle de la Lune (53). Si l’on adoptait cette hypothèse, poursuit Riccioli, il en découlerait les conséquences suivantes. «La» libration serait nulle dans les apsides ; de l’apogée au périgée, Grimaldi reculerait du bord oriental du disque, tandis que le Mare Crisium se rapprocherait du bord occidental ; inversement, du périgée à l’apogée, Grimaldi se rapprocherait du bord oriental, tandis que le Mare Crisium reculerait du bord occidental (54).

En réalité, retenu par l’observation des comètes qui parurent dans les années 1650-1653, dont on trouvera les traces, en 1668, dans la Cometographia, ce n’est qu’en 1654 que Hevelius prend connaissance de l’ouvrage de Riccioli, que lui avait communiqué Athanasius Kircher. Il s’aperçut, alors, que les phénomènes invoqués, que Riccioli faisait dépendre, à titre de conséquences éventuelles, d’une hypothèse formulée un peu au hasard et exprimée à l’irréel du présent (dont témoigne l’usage de l’imparfait du subjonctif), observaient, en réalité, rigoureusement la période qu’il avait touvée, de son côté, dès 1648, car, faire dépendre «la» libration de l’excentricité du cercle de la Lune, revenait à en faire une fonction de la différence angulaire entre l’anomalie vraie et l’anomalie moyenne de la Lune, donc, de l’équation. Ce rapport n’était valable, cependant, que pour une partie du mouvement libratoire, celle qui se fait d’occident en orient, et inversement. Hevelius se trouva, ainsi, conduit à dissocier, le premier, une libration, de période anomalistique, qui se fait en longitude, et une libration, de période draconitique, qui se fait en latitude. C’est dans ces conditions qu’il adresse à Riccioli l'Epistula de Motu Lunae libratorio (55).

Lorsque la Lune est dans ses apsides, la libration en longitude sera moyenne, ou nulle. L’axe du cône visuel, en corrigeant la parallaxe horizontale, se confond avec la ligne des apsides de la Lune (56).

Lorsque la Lune est à 90° d’anomalie moyenne, comptée depuis l’apogée, et que la section du globe lunaire par le plan qui, à l’apogée, passait par la ligne des apsides, rencontre celle-ci à angles droits, l’axe du cône visuel de l’observateur terrestre passe, sans corriger l’équation, par un point situé, à la surface du globe lunaire, à la distance angulaire a du point par lequel il passait à l’apogée. Par conséquent, l’ensemble des taches lunaires subit un décalage vers l’occident, d’une quantité angulaire égale à celle de l’équation. Le Mare Crisium se rapproche donc du bord occidental du disque, tandis que Grimaldi s’éloigne du bord oriental (57).

L’inverse a lieu à 270° d’anomalie moyenne. Cette fois, l’axe du cône visuel rencontre la surface du globe lunaire à une distance angulaire a à l’occident du point par lequel il passe dans les apsides, et les taches sont décalées, d’autant de degrés vers l’orient, que vers l’occident, à 90° d’anomalie. Aussi, le Mare Crisium est le plus loin possible du bord occidental du disque, tandis que Grimaldi est le plus près possible du bord oriental (58).

Cette situation suppose une disposition dans laquelle une même section du globe lunaire, telle AB, demeure dans un plan qui passe constamment par le centre M des moyens mouvements lunaires, c’est-à-dire où la Lune présente constamment la même face vers ce centre. Elle suppose, encore, que la quantité de l’excentricité CT du cercle de la Lune, ou, à défaut, celle de la distance MT, du centre de la Terre au centre des moyens mouvements lunaires, soit suffisante pour faire l’angle a égal à 8°. C’est la difficulté de satisfaire à cette dernière condition qui avait fait rejeter, par Riccioli, l’hypothèse suivant laquelle «la» libration dépend de l’excentricité du cercle de la Lune. Enfin, la libration en longitude doit présenter, dans cette hypothèse, une inégalité d’un peu moins de neuf ans, liée au mouvement des apsides lunaires (59). Or, c’est cette inégalité qui avait, dès 1648, conduit Hevelius à rattacher cette partie de la libration à la révolution anomalistique de la Lune (60).

La découverte de la période anomalistique de la libration en longitude conduit Hevelius à une refonte de la théorie de la libration dans son ensemble. Celle-ci revêtait, dans la Selenographia, l’aspect d’une théorie unitaire, où, comme, en 1645, chez Boulliau, ou, encore en 1651, chez Riccioli, «la» libration était pensée comme un phénomène global, justiciable d’une explication optique, faisant appel à des effets de perspective issus de la variation des hauteurs méridiennes de la Lune, par suite de son mouvement en déclinaison et de l’inégalité présentée par ce dernier en raison de la révolution des nœuds de la Lune en dix-huit ans et sept mois. Lorsqu’en 1648, Hevelius constate que la maxima libratio, c’est-à-dire l’instant où l’écart se creuse au maximum entre le Mare Crisium et la circonférence du disque, qu’il avait observée, en 1644, dans le Cancer, avait lieu dans le Capricorne, il conclut, logiquement, de cet écart de six signes en quatre ans, à une inégalité de huit ans, dont ne pouvait rendre compte le mouvement des nœuds, qui ne s’élevait, pour la même période qu’à 4 x 360 / 18 = 80°. C’est donc l’observation de l’inégalité de leur mouvement, qui permet à Hevelius de rattacher, à la révolution, directe, des apsides, dont la période est de plus de huit ans, la libration de taches comme Mare Crisium et Grimaldi, i. e. des taches voisines du bord occidental et du bord oriental du disque lunaire. Dans ces conditions, la libration en latitude se présente, en quelque sorte, comme un mouvement résiduel, obtenu par soustraction de la libration en longitude et dont l’étude est conduite d’après l’observation de la variation de l’inclinaison du terminateur dans les quadratures, donc, sur le modèle de ce que nous avions appelé, chez Galilée, la libration «annuelle», à l’élaboration théorique de laquelle Hevelius avait donné un certain développement dans la Selenographia (61). La conception des relations entre cône visuel et cône d’illumination, que développaient ces pages, se trouve donc reprise dans l’écrit de 1654, à ceci près qu’elle se donne, désormais, pour la théorie d’une libration en latitude, obtenue par soustraction d’une libration en longitude de période anomalistique, dans les conditions de la découverte de l’inégalité de huit ans de cette dernière. Si, dans ces conditions, il ne fait guère de doute, comme montre sa réaction à la lecture de Riccioli, que Hevelius ait reconnu, à cette dernière, une nature optique, il devient, en revanche, assez délicat de savoir si la première revêt, dans son esprit, la signification d’une apparence optique ou d’une réalité physique. Rien, dans ses déclarations explicites, n’autorise à conclure qu’il ait accordé, à la libration en latitude, une signification autre qu’optique, mais nous verrons que semblable position conduit à d’insoutenables antinomies, ainsi qu’il n’échappera, ni à ses contemporains, ni à ses successeurs.

La Lune tourne autour de la Terre, en vingt-sept jours et sept heures, dans un plan qui est incliné, au plan de l’écliptique, d’environ cinq degrés. L’axe de l’orbite lunaire coupe, donc, l’axe de l’écliptique, et une droite menée, par le centre du globe lunaire, orthogonalement au plan de l’orbite lunaire, une droite menée, par ce centre, orthogonalement au plan de l’écliptique, sous un angle de cinq degrés. En prenant en considération, non la révolution sidérale de la Lune, mais sa révolution draconitique, c’est-à-dire son retour périodique, non à la même longitude, mais à son nœud ascendant, un plan, conduit par les deux droites parallèles, l’une, à l’axe de l’écliptique, l’autre, à celui de l’orbite lunaire, orthogonalement au plan de l’écliptique, demeure parallèle à lui-même au cours d’une révolution de la Lune autour de la Terre. Un tel plan est un plan remarquable, au sens où nous avions appelé remarquable, par sa double appartenance au système lié à l’observateur terrestre, et au système indépendant de cet observateur, le plan qu’on pouvait, seul, mener par l’axe de rotation du Soleil, perpendiculairement au plan de l’écliptique, et qui était le seul plan orthogonal, à la fois, au plan de l’écliptique et au plan de rotation du Soleil. Il est, en effet, lui aussi, le seul plan qu’on peut mener, par une droite tracée, par le centre du globe lunaire, parallèlement à l’axe de l’orbite, orthogonalement au plan de l’écliptique. De même que le disque du Soleil n’était dans le plan remarquable du Soleil, que dans les stationes rectilineae, le disque de la Lune n’est, dans le plan remarquable de la Lune, que dans les nœuds. Ces dernières conditions sont les seules où, l’axe du cône visuel de l’observateur terrestre venant rencontrer, à angles droits, le plan remarquable de la Lune, les deux droites menées par le centre du globe lunaire paraissent, à cet observateur, se couper sous un angle de cinq degrés. La section du globe lunaire par la base du cône visuel de l’observateur terrestre est dans le plan remarquable ; les «pôles» de l’orbite lunaire et de l’écliptique, ou, plus exactement, des droites, menées par le centre du globe lunaire, qui leur sont parallèles, sont situés sur la section du globe par le plan de la base du cône visuel, le «pôle» Nord de l’orbite, à cinq degrés à l’occident du «pôle» Nord de l’écliptique, dans le nœud ascendant, et à l’orient, dans le nœud descendant (62). Lorsque la Lune est à 90° de ses nœuds, le plan mené par ces deux droites passe par le centre de la Terre (63). Les deux droites paraissent alors se confondre aux yeux de l’observateur terrestre. La section du globe lunaire par la base du cône visuel est toujours dans un plan orthogonal au plan de l’orbite lunaire ; les axes de l’orbite et de l’écliptique conservant leurs relations réciproques au cours d’une révolution de la Lune autour de la Terre, le «pôle» Nord de l’écliptique sera dans l’hémisphère caché, en arrière du «pôle» Nord de l’orbite, à cinq degrés de latitude Nord (c'est le cas désigné par le caractère B, dans la figure), et dans l’hémisphère apparent, en avant du «pôle» Nord de l’orbite, à cinq degrés de latitude Sud (cas désigné par le caractère C) ; le «pôle» Sud de l’écliptique, dans l’hémisphère apparent, en avant du «pôle» Sud de l’orbite, à cinq degrés de latitude Nord, et dans l’hémisphère caché, en arrière du «pôle» Sud de l’orbite, à cinq degrés de latitude Sud (64). Ces considérations rendent bien compte des apparences de la libration en latitude. En effet, si les deux droites paraissent, aux yeux de l’observateur terrestre, se couper, sous un angle de cinq degrés, lorsque la Lune est dans ses nœuds, le pôle Nord de l’orbite lunaire, transposé dans le globe de la Lune, se présentera, sur la circonférence du disque, à cinq degrés à l’occident du pôle Nord de l’écliptique, dans le nœud ascendant, et à l’orient, dans le nœud descendant (65).

Il convient, toutefois, de faire observer que, si, dans le cas du Soleil, le système de coordonnées, indépendant de l’observateur, est celui du plan de rotation, et le système, lié à l’observateur, celui de l’écliptique, dans le cas de la Lune, le système, indépendant de l’observateur, est celui de l’écliptique, et le système, lié à l’observateur, celui de l’orbite lunaire. Le disque de la Lune fait partie du système de l’orbite, comme le disque du Soleil, du système de l’écliptique. C’est que, dans les deux cas, le cône visuel se définit dans les coordonnées du plan de révolution, celui de l’écliptique, dans le cas du Soleil, celui de l’orbite, dans le cas de la Lune. Lorsque la Lune est dans l’une de ses plus grandes latitudes, ce sont donc les pôles de l’écliptique, transposés dans le globe lunaire, qui sont, alternativement, dans l’hémisphère apparent et dans l’hémisphère caché, le pôle Nord, dans l’hémisphère caché, et le pôle Sud, dans l’hémisphère apparent, à +5°, le pôle Nord, dans l’hémisphère apparent, et le pôle Sud, dans l’hémisphère caché, à -5°. Et c'est sur ce point précis que la théorie classique de la libration, qu'on attribue, d'ordinaire, à Cassini, s'articule à celle, préclassique, de Hevelius.

Il s’agit, tout d’abord, de déployer, dans toutes ses conséquences, l’idée suivant laquelle, lorsqu’on est en présence de deux systèmes d’axes, l’un, lié à l’observateur terrestre, l’autre, indépendant de l’observateur, en mouvement angulaire l’un à l’égard de l’autre, on ne peut concevoir qu’un seul plan qui soit orthogonal, à la fois, au plan de référence de chacun des deux systèmes d’axes (ou qu’on ne peut mener qu’un seul plan par l’axe des z des deux systèmes). Dans le cas où l’un des deux systèmes d’axes est en mouvement angulaire par rapport à l’autre, cette situation ne va pas sans que ce plan présente, en un sens, un mouvement de révolution d’une quantité égale à celle du mouvement angulaire de l’un des deux systèmes par rapport à l’autre.

Une analogie empruntée à l’astronomie sphérique peut faciliter l’intelligence de ce qui est en cause. Supposons que les deux systèmes d’axes en mouvement angulaire l’un par rapport à l’autre soient le système des coordonnées horizontales et le système des coordonnées équatoriales. Si, en un instant donné, il n’y a qu’un seul cercle de hauteur (dans un plan orthogonal au plan de l’horizon) qui coïncide avec un cercle de déclinaison (dans un plan orthogonal au plan de l’équateur), ce dans le plan du méridien du lieu, il n’en demeure pas moins qu’en des instants successifs, ce sont différents cercles de déclinaison qui «entrent», à tour de rôle, dans le plan du méridien. Au cours de la révolution diurne, tous les cercles de déclinaison occupent, ainsi, successivement, le plan du méridien et, de ce fait, aux yeux d’une cosmologie qui rapporte les mouvements au site de l’observateur et pour laquelle la vision est discriminatoire au regard du mouvement et du repos, accomplissent une révolution à l’égard de ce point privilégié qu’est le centre de la sphère céleste. De semblables considérations avaient conduit Scheiner à attribuer une révolution physique à l’unique plan qu’on peut mener par l’axe de rotation du Soleil, perpendiculairement au plan de l’écliptique.

Le cas de la Lune n’est pas différent de celui du Soleil. Tout comme, indépendamment de la rotation du Soleil en vingt-sept jours, un plan mené par un diamètre quelconque du globe solaire, perpendiculairement au plan de l’écliptique, conserve sa direction initiale et demeure parallèle à lui-même au cours d’une révolution de la Terre autour du Soleil, «qui produit le même effet que ferait une révolution du Soleil autour de la Terre», un plan mené par un diamètre quelconque du globe lunaire, perpendiculairement au plan de l’orbite lunaire, conserve sa direction initiale et demeure parallèle à lui-même au cours d’une révolution de la Lune autour de la Terre. Or, par le diamètre d’une sphère, on peut tracer une infinité de plans, perpendiculairement au plan que ce diamètre rencontre à angles droits. Ainsi, par la verticale d’un lieu, on peut mener une infinité de cercles verticaux, perpendiculairement au plan de l’horizon ; par l’axe du monde, une infinité de cercles de déclinaison, perpendiculairement au plan de l’équateur ; et, par l’axe de l’écliptique, une infinité de cercles de latitude, perpendiculairement au plan de l’écliptique. Tout comme la verticale du lieu est l’intersection commune des plans de tous les cercles verticaux, l’axe du monde, des plans de tous les cercles de déclinaison, et l’axe de l’écliptique, des plans de tous les cercles de latitude, le diamètre quelconque d’une sphère est ainsi l’intersection commune d’une infinité de plans perpendiculaires au plan qu’il rencontre à angles droits. Si l’on peut ainsi mener une infinité de plans par le diamètre quelconque d’une sphère, diamètre qui est leur intersection commune, on ne peut, en revanche, en mener qu’un seul par deux diamètres de la sphère inclinés l’un à l’autre. Ainsi il n’y a qu’un seul plan perpendiculaire, à la fois, au plan de l’horizon d’un lieu et au plan de l’équateur du monde, celui du méridien du lieu, qui est, à la fois, cercle vertical et cercle de déclinaison, tout comme il n’y a qu’un seul plan perpendiculaire, à la fois, au plan de l’équateur et au plan de l’écliptique, celui du colure des solstices, qui est, à la fois, cercle de déclinaison et cercle de latitude. Tout comme le méridien est un demi-cercle (plutôt qu’un cercle), passant, à la fois, par le zénith et par les pôles du monde, dans un plan qui est, seul, perpendiculaire, à la fois, au plan de l’horizon et au plan de l’équateur, et le colure des solstices, un cercle, passant, à la fois, par les pôles du monde et par les pôles de l’écliptique, dans un plan qui est, seul, perpendiculaire, à la fois, au plan de l’équateur et au plan de l’écliptique, le plan mené par deux diamètres quelconques d’un globe est le seul à être perpendiculaire, à la fois, aux deux plans menés par le centre du globe, perpendiculairement à chacun des deux diamètres. Dans ces conditions, il n’est donc possible de mener, par tout diamètre du globe solaire, autre que la normale au plan de l’écliptique, qu’un seul plan qui soit perpendiculaire au plan de l’écliptique, tout comme, par un diamètre du globe lunaire, autre que la normale au plan de l’orbite, qu’un seul plan qui soit perpendiculaire au plan de l’orbite lunaire. Il revient donc au même de dire que, par un diamètre quelconque du globe, on ne peut mener qu’un seul plan qui soit perpendiculaire, au plan de l’écliptique, dans le cas du Soleil, et au plan de l’orbite, dans le cas de la Lune, ou que, par un diamètre quelconque du globe, on ne peut mener qu’un seul plan qui passe, en même temps, par le diamètre perpendiculaire, au plan de l’écliptique (ou : par le diamètre, parallèle à l’axe de l’écliptique), dans le cas du Soleil, au plan de l’orbite (ou : parallèle à l’axe de l’orbite), dans le cas de la Lune.

Or, d’une part, les directions de l’axe de l’écliptique, dans le cas du Soleil, et de l’axe de l’orbite, dans le cas de la Lune, sont constantes, si l’on ne tient pas compte, de la précession des équinoxes, dans le cas du Soleil, du mouvement rétrograde des nœuds de l’orbite, dans le cas de la Lune. Sont, donc, constantes, également, l’inclinaison de l’écliptique, et celle de l’orbite lunaire, à l’égard d’un plan fixe. D’autre part, le disque apparent est toujours dans un plan perpendiculaire, au plan de l’écliptique, dans le cas du Soleil, de l’orbite lunaire, dans le cas de la Lune. Dans ces conditions, indépendamment de tout autre mouvement (nous disons : indépendamment de tout autre mouvement, pour exclure, par hypothèse, tout mouvement de rotation, tant dans le cas du Soleil, que dans le cas de la Lune), un plan passant, à la fois, par un diamètre quelconque du globe et par l’axe, de l’écliptique, dans le cas du Soleil, de l’orbite lunaire, dans le cas de la Lune, conserve sa direction initiale et demeure parallèle à lui-même au cours d’une révolution, tropique, dans le cas du Soleil, draconitique, dans le cas de la Lune. Il instaure, de ce fait, un déplacement angulaire à l’égard du plan de la base du cône visuel de l’observateur terrestre, plan qui, tout en demeurant constamment perpendiculaire au plan, de l’écliptique, dans le cas du Soleil, de l’orbite, dans le cas de la Lune, et tout en passant constamment par le diamètre du globe parallèle à l’axe, de l’écliptique, dans le cas du Soleil, de l’orbite, dans le cas de la Lune, n’en pivote pas moins, en quelque sorte, sur cet axe et occupe, à son égard, toutes les positions angulaires possibles au cours de la révolution de l’astre autour de la Terre, tout comme, par l’effet de son mouvement en longitude, cet astre occupe, lui-même, successivement, tous les cercles verticaux, tous les cercles de déclinaison ou tous les cercles de latitude. Et, de même que les plans de tous les cercles verticaux se coupent dans la verticale du lieu, les plans de tous les cercles de déclinaison, dans l’axe du monde, ou les plans de tous les cercles de latitude, dans l’axe de l’écliptique, les plans des sections successives du globe par le plan de la base du cône visuel de l’observateur terrestre se coupent dans le diamètre du globe orthogonal, au plan de l’écliptique, dans le cas du Soleil, de l’orbite lunaire, dans le cas de la Lune. Comme ce même diamètre est dans le seul plan qu'on peut mener par un diamètre quelconque du globe, orthogonalement au plan, de l’écliptique, dans le cas du Soleil, de l’orbite, dans le cas de la Lune, ce plan, ayant, ainsi, une direction constante, présente un mouvement angulaire à l’égard de l’observateur terrestre, par l’effet duquel le globe lui paraît accomplir une révolution complète, dans le sens rétrograde, sur un axe parallèle à l’axe, de l’écliptique, dans le cas du Soleil, de l’orbite, dans le cas de la Lune, en une année tropique, dans le cas du Soleil, en un mois draconitique, dans le cas de la Lune (66).

Lorsque, le deux mai 1675, Cassini présente sa théorie de la libration à l’Académie royale des sciences, le compte-rendu de l’historien officiel de l’Académie relève l’importance de l’expression «colurus Lunae proprius» (67). Nous pouvons, maintenant, préciser le contenu de cette notion et soupçonner les raisons du choix de ce terme. L’expression de «colure de la Lune» désigne une section du globe lunaire par un plan perpendiculaire, à la fois, au plan de révolution et de rotation de la Lune. Dans le cas du Soleil, en effet, les apparences observées dans le disque, telles les trajectoires des taches, leurs courbures et rectifications, s’expliquent aisément par la combinaison de l’hypothèse précédente d’une révolution optique, apparente, du globe solaire, dans le sens rétrograde, dans le plan de l’écliptique, en une année tropique, avec celle d’une rotation du globe, dans le sens direct, dans un plan incliné au plan de révolution d’une certaine quantité, avec une période appropriée. Celle-ci s’obtient en multipliant par deux le temps mis par les taches à parcourir l'espace qui sépare le bord oriental du bord occidental du disque solaire, soit 2 x 13,5 = 27 jours ; la quantité de l’inclinaison du plan de rotation au plan de révolution est donnée par l’angle des trajectoires des taches à l’égard de l’écliptique dans les rectifications, soit, selon Scheiner, sept degrés et demi. La théorie se trouve facilitée, dans le cas du Soleil par la circonstance de la discordance des périodes des deux mouvements, de révolution et de rotation, de 365, 25 j., dans le cas de la révolution, et de 27 j., dans le cas de la rotation ; de ce fait, le mouvement des taches saute aux yeux avec une évidence qui fait d’emblée conclure à une rotation du globe sur lui-même. Les rectifications et incurvations des trajectoires des taches, les stationes et les aequilibria, renvoient, de leur côté, au mouvement de révolution, comme prouve l’usage auquel les fait servir Galilée, dans la Terza Giornata, et la signification physique que leur avait reconnue Scheiner est, simplement, le signe que le seul plan qu’il est possible de mener, par l’axe de rotation du Soleil, perpendiculairement au plan de l’écliptique, conserve sa direction initiale et demeure constament parallèle à lui-même au cours d’une révolution tropique du Soleil, tout comme il est, naturellement, soumis à la précession des équinoxes et accomplit, de ce fait, une révolution complète, à l’égard de la sphère des fixes, avec la période de la révolution de la huitième sphère.

Dans le cas de la Lune, l’égalité des périodes de révolution et de rotation avait eu pour effet de brouiller considérablement, aux yeux de Hevelius et de Boulliau, les relations exactes entre les mouvements du globe lunaire. Nous avons vu, ainsi, Hevelius aboutir, à deux reprises, à l’occasion de l’étude des relations du cône visuel de l’observateur terrestre avec le cône d’illumination et les sections du globe lunaire dans les quadratures, dans la Selenographia, et à l’occasion de la libration en latitude, dans l’Epistula de Motu Lunae libratorio, à l’idée qu’un plan mené par le diamètre du globe lunaire parallèle à l’axe de l’écliptique, perpendiculairement au plan de l’orbite lunaire, conserve une direction constante et demeure constamment parallèle à lui-même, sans que ces conditions impliquassent, à ses yeux, une rotation compensatrice qu’il persiste à refuser dans le cas de la Lune. Il nous semble qu’en l’occurrence, Cassini ait procédé par analogie à l’égard de la théorie du Soleil, telle qu’il pouvait la trouver chez Scheiner (68). Le point de départ de sa conception du mouvement de la Lune est, à n’en pas douter, dans la théorie de la libration en latitude de Hevelius. Celle-ci a reconnu un fait essentiel : deux diamètres du globe lunaire parallèles, l’un, à l’axe de l’orbite lunaire, l’autre, à l’axe de l’écliptique, conservent leurs directions initiales et demeurent dans un plan qui reste constamment parallèle à lui-même au cours d’une révolution draconitique de la Lune. Ces conditions, d’une part, font ressortir l’analogie de la théorie de la Lune et de celle du Soleil, d’autre part, obligent à penser le mouvement de la Lune dans le concept d’une révolution de roulement. A ce stade intervient alors l’idée d’une rotation de la Lune, idée qui, dans l’esprit de Cassini, renvoie à une triple origine : l’analogie de la théorie du Soleil de Scheiner, l’égalité des périodes invoquée par les tenants de l’épicycle lunaire et refusée par Buridan, enfin, l’égalité des périodes de révolution et de rotation, invoquée, puis, écartée, par Boulliau, dont une lettre de Cassini à Gassendi laisse penser qu’il peut avoir connu l’Astronomia philolaïca (69). La détermination de la période draconitique de la rotation de la Lune renvoie, de nouveau, à la théorie de la libration en latitude de Hevelius, que cette découverte d’une rotation du globe lunaire permet à Cassini de corriger sur un point important. Hevelius avait été induit en erreur, dans l’Epistula de Motu Lunae libratorio, en ayant sans cesse présente à l’esprit l’explication, développée dans la Selenographia, de l’inclinaison des sections lunaires dans les quadratures par les relations constantes de l’axe de l’orbite lunaire et de l’axe de l’écliptique : Cassini corrige la théorie de la libration en latitude, en montrant que ce phénomène est produit, non par les relations constantes de l’axe de l’orbite lunaire à l’égard de l’axe de l’écliptique, mais à l’égard de l’axe de rotation. La quantité de l’inclinaison du plan de rotation à l’égard du plan de révolution, de sept degrés et demi, fait évidemment penser à celle du plan de rotation du Soleil à l’égard du plan de l’écliptique, dans la théorie de Scheiner (70), mais elle se rapporte également à d’autres discussions contemporaines, que reflètent un passage de l’Epistula de Motu Lunae libratorio (71), une lettre de Boulliau à Hevelius, du vingt-trois juillet 1655 (72), et un texte de l’Astronomia reformata de Riccioli (73). Enfin, même si la libration en latitude observée par Hevelius est produite par la conservation de la direction, non d’un plan passant par l’axe de l’orbite lunaire et par l’axe de l’écliptique, mais d’un plan passant par l’axe de l’orbite et par l’axe de l’équateur lunaire, ce plan n'en doit pas moins observer la même direction que celui invoqué par Hevelius. Il en résulte que les équinoxes lunaires coïncident avec les noeuds de la Lune, et que la quantité de la précession lunaire est égale à celle de la révolution de ces nœuds (74). Laplace demeure donc fidèle à la pensée de Cassini lorsqu’il dit, dans le langage de son époque, que, si l’on mène, par le centre du globe lunaire, un plan parallèle au plan de l’écliptique, le plan de l’orbite lunaire, le plan mené par le centre de la Lune, parallèlement à l’écliptique, et le plan de l’équateur lunaire conservent toujours une intersection commune (75), le second de ces trois plans étant engendré par la révolution, en dix-huit ans et sept mois, dans le sens rétrograde, de l’intersection commune qui est, à la fois, la ligne des nœuds et la ligne des équinoxes de la Lune. La coïncidence des nœuds et des équinoxes est, ainsi, la conséquence directe de la conservation de la direction initiale du plan mené par l’axe de l’orbite, perpendiculairement au plan de l’écliptique, postulée par Hevelius. En dépit de la remarque de Cassini sur les stravaganze del dottissimo Evelio (76), sa théorie dépend donc étroitement de celle de son devancier.

Si des liens étroits rattachent, ainsi, la théorie de Cassini à celle de Hevelius, au point qu’on peut qualifier la première de lecture de la seconde à la lumière de la théorie du Soleil de Scheiner, la question demeure ouverte de ses rapports à la version initiale, refusée par l’auteur, de la théorie de Boulliau. Nous avons vu que cette première version de la théorie de Boulliau reposait sur l’idée de la conservation d’une direction constante de l’axe de l’orbite de la Lune, engendrant une révolution apparente du globe lunaire sur lui-même, dans le sens rétrograde, compensée par une rotation physique, de sens direct, de période égale. Tous ces traits se retrouvent dans la théorie de Cassini, et il n’aura finalement manqué à Boulliau que d’avoir déterminé le plan dans lequel s’effectue cette rotation et la quantité de son inclinaison au plan de l’orbite. La question est donc posée de savoir si Cassini a pu avoir connaissance de cette première théorie de Boulliau.

Nous pourrions nous limiter à renvoyer à la lettre de Cassini à Gassendi, qui voit, en Boulliau, l’un des phares, à l’égal de Kepler, de l’astronomie, et y voir l’indice d’une lecture attentive, de la part de Cassini, de l’Astronomia philolaïca, parue huit ans plus tôt et où figure la première version de la théorie de Boulliau. Toutefois, cette mention élogieuse de Boulliau par Cassini, mettant sur le même plan Boulliau et Kepler, nous paraît renvoyer, de ce fait, à la théorie des planètes, pour laquelle le manuscrit de la Ptolemaïca Methodus, de 1669, prouve que Cassini éprouvait un vif intérêt. Nous avons donc à nous demander si Cassini a pu subir l’influence de Boulliau au cours de l’élaboration ultérieure qui devait conduire ce dernier à la dissociation conceptuelle de la libration en longitude et de la libration en latitude et à la reconnaissance de la période anomalistique de la dernière. Nous avons donc à étudier, successivement, les sources permettant de dater les différents moments de l’élaboration de la doctrine de Boulliau sur la libration et de préciser ses rapports avec l’élaboration parallèle de la doctrine de Hevelius. Nous étudierons ensuite les documents attestant les rapports de Boulliau et de Cassini.

Il est entendu que les versions successives des théories de Boulliau et de Hevelius tiennent à la lente reconnaissance de la période anomalistique attribuée à la libration en longitude et à la dissociation conceptuelle qui s’opère, parallèlement, entre libration en longitude et libration en latitude (Hevelius, en 1647, dans la Selenographia, comme Boulliau, en 1645, dans l’Astronomia Philolaïca, parlait encore d’une seule libration de la Lune), cependant que les modèles théoriques, qui retiennent, au premier chef, notre attention, ne subissent que peu de modifications.

Quatre lettres adressées à Hevelius nous permettent de nous faire une idée des progrès qui s’accomplissent dans l’esprit de Boulliau au cours des années 1648-1650. A l’origine de sa réflexion se trouvent des observations du Mare Crisium et la question des rapports que son mouvement en libration entretient avec celui des taches situées vers les bords Nord et Sud du disque lunaire. Nous avons vu à quel point la doctrine de la Selenographia était, sur ce point, peu satisfaisante. Le onze décembre 1648, Boulliau écrit à Hevelius que «la période de la libration de la Lune ne lui paraît pas encore établie avec précision» (77). Le sept janvier 1650, il lui écrit qu’ «une idée (ennoia, en grec dans le texte) lui est venue», idée qui consiste à considérer l’origine de «la» libration comme mobile, au lieu de la rattacher à un point fixe du zodiaque (78). Il ajoute qu’il a bon espoir de pouvoir, grâce à cette «ennoia», rattacher, au mouvement propre de cette origine, les incohérences que décelaient les observations dans les mouvements du Mare Crisium. On voit s’annoncer, ici, l’idée d’une période anomalistique de «la» libration, entendons de celle du Mare Crisium, la libration en longitude : les incohérences que révèlent les observations peuvent s’expliquer, si l’on admet que le mouvement du Mare Crisium doit être rapporté, non à un point fixe du zodiaque, mais à une origine elle-même mobile à l’égard d’un point fixe. Sans doute, pour le moment, Boulliau ne dit pas que cette origine est l’apogée, et l’anomalie, l’argument de l’inégalité de la libration. Mais, si le concept d’une période anomalistique de «la» libration n’est pas formulé, les observations que, dans ses lettres, il cite à l’appui de ses conclusions ne laissent aucun doute quant à savoir que Boulliau est bien sur la voie de la découverte que la libration en longitude est une fonction de l’anomalie. Le dix-huit avril de la même année, il annonce à son correspondant qu’il a l’intention de soumettre «sous peu» son hypothèse «au calcul». Nous verrons qu’une lettre rédigée en des termes fort analogues a été adressée à Cassini le trente janvier 1654. Enfin, la lettre de Boulliau à Hevelius du vingt-trois juillet 1655, qui est une réponse à l’envoi de l’Epistula de Motu Lunae libratorio, nous apprend deux choses : d’abord, que l’explication proposée par Hevelius, dans ce texte, est conforme à l’ennoia de Boulliau de 1650 et, par suite, qu’il s’agit bien, dans ce dernier cas, de l’hypothèse d’une période anomalistique de la libration en longitude ; ensuite, elle nous renseigne sur les dates respectives auxquelles cette période a été découverte par Hevelius et par Boulliau, puisque Hevelius, qui, dans son texte imprimé, indiquait la date de 1648, est dit, par Boulliau, l’avoir devancé de trois ans. En admettant que Boulliau compte, parmi les trois années, l’année en cours au moment de la découverte, cette donnée confirme la date de 1650 que nous avait fournie l’étude de la correspondance de Boulliau. Nous pouvons donc considérer que la période anomalistique du mouvement libratoire du Mare Crisium a été reconnue, indépendamment, en 1648, par Hevelius et, en 1650, par Boulliau. Nous avons vu que les apparitions de comètes des années 1650-1653 ont retenu Hevelius de publier sa découverte. Cette publication survint seulement en 1654 et se présente sous la forme de la lettre ouverte à Riccioli, à propos d’une remarque de l’Almagestum novum. Elle rendit superflue celle de Boulliau sur le même sujet.

Riccioli répond à la lettre ouverte par une lettre, manuscrite, à Hevelius du vingt-quatre février 1655. Dans cette lettre, Riccioli fait état d’une lettre de Boulliau, dont le destinataire, n’étant pas, au vu de la tournure employée : Bononiam scripsit, Riccioli lui-même, pourrait bien être, croyons-nous, Cassini. Rappelons que, né à Perinaldo, dans le comté de Nice, ayant reçu son instruction chez les Jésuites de Gênes, ce dernier occupe, depuis 1650, la chaire laissée vacante par la mort de Cavalieri, à l’Archiginnasio de Bologne. Or, nous connaissons trois documents (79), dont la conjonction nous paraît autoriser d’identifier une lettre de Boulliau à Cassini, du trente janvier 1654, comme étant la lettre un peu mystérieuse dont parle ici Riccioli.

Dans une lettre à Storani du vingt février 1654, Boulliau indique à son correspondant qu’il a reçu, de Cassini, une lettre, accompagnée d’une théorie (manuscrite) des comètes. Nous connaissons, de fait, dans le recueil factice coté V. 238 de la Réserve des Imprimés de la Bibliothèque nationale de Paris, recueil relatif aux comètes des années 1650-1653, une lettre de Boulliau adressée à Cassini, du dix-huit juillet 1653, où il lui demande de lui communiquer ses observations de la plus récente de ces comètes et lui demande s’il a observé une certaine éclipse de lune, qu’il s’agisse de celle de septembre 1652 ou, plutôt, de celle de mars 1653. Le vingt et un octobre, Cassini lui répond par une lettre datée de Perinaldo, à laquelle était jointe la précieuse théorie manuscrite des Comètes qui, distraite du tome XIX de la Collection Boulliau du département des manuscrits à une date que nous ne saurions préciser, dort, depuis, parmi les vaticinations du Pseudo-Argolin, dans le recueil factice de la Réserve des Imprimés (80). Or, voici ce qu’on lit dans la réponse de Boulliau, datée du trente janvier 1654 : «Tandem reperi (lege : repperi) terminum revolutionis librationis corporis Lunaris, & brevem tractatum ea de re in lucem emittam, si per tricas & negotia Musis inimica & infesta licuerit.». En post-scriptum, il lui demande de saluer Riccioli, «quod in (...) Almagesto saepissime nomen meum tam honorifice repetat.». Et lorsque, le vingt-quatre février 1655, Riccioli prie Hevelius de l’excuser de lui répondre en si peu de mots, «praesertim cum Bullialdus huc Bononiam scripsisset deprehendisse iam omnia quae spectant ad hoc negotium, ac brevi vulgaturum», il pourrait bien s’agir de cette lettre de Boulliau à Cassini du trente janvier 1654. Ces documents, à vrai dire, nous apprennent peu de choses. Les termes employés par Riccioli, dans sa lettre à Hevelius du vingt-quatre février 1655 semblent bien indiquer que les astronomes bolonais attendaient toujours, à cette date, l’ouvrage annoncé par Boulliau et qu’ils n’avaient aucune connaissance de son contenu. Il reste donc peu d’espoir de découvrir, un jour, dans quelque recueil factice de la Bibliothèque de l’Archiginnasio, une théorie de la libration de Boulliau comparable, en importance, à l’écrit de Hevelius de 1654. On peut même être sensible comme à une nuance de regret qui perce dans les dernières lignes de la lettre de Riccioli à Hevelius du vingt-quatre février 1655 : «Noli autem mirari si nunc tam paucis respondeam humanissimis tuis et literis et muneribus. Nam P. Grimaldi observationes librationis Lunaris, ad hunc usque diem continuatas, nondum plane digessimus, praesertim cum Bullialdus huc Bononiam scripsisset...etc.» (81). A la différence de Boulliau, qui, dans sa réponse à Hevelius, du vingt-trois juillet 1655, déclare n’avoir rien à reprendre aux explications de son correspondant et qui renonce à une publication pour son compte, à la différence aussi de Cassini, qui saura en tirer des conséquences insoupçonnées, il ne semble pas que Riccioli ait eu pleinement conscience de l’importance de l’écrit de Hevelius de 1654 et, de fait, ses propres déclarations à ce sujet, en 1665, dans l’Astronomia reformata, sont, à cet égard, éloquentes, sans que cette situation autorise de conclusions quant à la datation de la théorie de Cassini, qui semble bien constituée en 1668 (82).